sutton 교수의 Reinforcement Learning An Introduction을 읽고 공부하기
Exercise 3.1 MDP 프레임워크에 맞는 자신만의 세가지 예제를 생각해보자. states, actions, rewards들을 확인하자. 가능한 각각 다른 예제로 세개 만들어보자. MDP 프레임워크는 추상적이고 유연하며 다양한 방법으로 적용할 수 있다.
첫번째로 자전거 문제를 생각해 볼 수 있을듯. action = 핸들을 꺾는 각도, 좌/우. state = 자전거의 속력, 좌/우로 기울어진 각도. reward = 속력이 증가하면 +1, 속력이 0이되면 negative reward
두번째: 온도 자동 조절 에어컨. action = 온도를 올리거나 내리거나. state = 현재 온도, 습도, 밖의 기온 등. reward = 사용자가 만족하면 +1, 불만족하면 negative reward
세번째: 게임의 ai 플레이어(ex. 슈퍼마리오). action = 슈퍼마리오가 할 수 있는 행동들(점프, 좌, 우 이동). state = 마리오의 현재 위치, 피해야하는 장애물들의 위치. reward = 목적지까지 제대로 가면 +1, 장애물을 만나면 negative reward
Exercise 3.2 MDP 프레임워크가 모든 목표지향적 문제를 유용하게 나타내는데 적합할까? 명확한 예외가 있는가?
MDP 프레임워크로 모든 강화학습 문제에 적용할 수는 없다고 배웠음. 모든 목표지향적 문제를 잘 나타낼 수 있을까? 이것 역시 그럴 순 없을 것 같은데 명확한 예외는 잘 모르겠네....
Exercise 3.3 운전하는 문제를 생각해보자. action을 액셀, 휠, 브레이크 즉, 몸과 자동차가 만나는 지점들을 action으로 정의할 수 있다. 또는 더 멀리 생각할 수도 있다. 타이어가 도로와 만나는걸 생각하면 action을 타이어 토크로 생각할 수도 있다. 여기서 더 멀리가면 머리와 몸으로 생각할 수도 있다. 이때 action은 손발을 제어하는 근육이다. 더 높은 레벨로 가면 사람의 action은 어디로 운전해 갈 것인가가 될 수 있다. 올바른 level은 무엇이며 에이전트와 환경 사이에 경계선을 어떻게 그려야할까? 그 경계선이 그려지는 근본적인 이유가 있는가? 아니면 자유로운 선택인가?
풀어야하는 문제가 무엇이냐에 따라서 경계선이 달라지지 않을까. 책의 내용처럼 하나의 로봇은 여러가지의 센서로 이루어져있고 각각이 하나의 에이전트다. 이 문제에서도 가장 높은 레벨에서는 action을 통해 어디로 운전해 갈지 결정하는 에이전트가 따로 있을 것이고 그 하위 레벨에서 손발을 제어하는 에이전트가 있을 것이다. 더 밑으로 내려가면 액셀, 휠, 브레이크 등을 action으로 사용하는 에이전트가 있을 것이다.
환경-에이전트의 경계선은 각각의 에이전트가 갖는 action, state, reward에 따라 다른 경계선을 가질 것이다. 경계선을 자유롭게 그린다고 할 수가 있을까? 그건 아닌듯
Exercise 3.4 example 3.3과 비슷한 표를 p(s',r | s,a)에 대해서 제시해라. s, a, s', r 및 p(s', r | s, a) 열과 p(s', r | s, a) >0인 모든 4개의 튜플인 행이( row for every 4-tuple for which p(s', r | s, a) >0 ) 있어야 한다.
Example 3.3이 뭐였는지 다시 보고 표를 그려보자

s, a, s', r을 열로 써서 다시 표를 그림. 이때 reward를 얻을 확률은 \( \theta \)로 고정 그렇다면 아래의 표가 나옴

열에서 고려하는 reward의 경우 expected reward가 아니기 때문에 실제로 에이전트가 얻을 수 있는 reward를 넣어봤음. 그래서 reward를 얻을 확률을 \( \theta \)라고 생각했음.
그리고 low에서 search를 했는데 high로 간 경우는 배터리가 방전되서 -3을 reward로 얻는 경우 밖에 없기때문에 이 경우는 빈 깡통을 발견했던 말던 reward를 -3으로 고정.
Exercise 3.5 섹션 3.1의 등식은 continuning 경우 이므로 episodic task에 적용시키기 위해 약간 수정해야 한다. (3.3)의 수정된 버전을 제공해 필요한 수정사항을 보여라.
이때 등장하는 3.3의 식
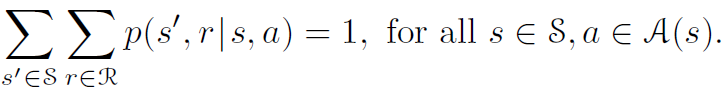
이거를 episodic task에 맞게 조금만 수정하는게 목표

다음과 같이 state와 action에 타임스텝 t를 아래첨자로 넣어주자. 그리고 \( t \neq \infty \) 이 조건을 추가해주면 될듯?
Exercise 3.6 폴-균형 문제를 실패했을 때 -1, 나머지 모든 reward는 0, discounting을 사용하는 episodic task라 생각하자. 그러면 각 타임스텝마다 return은 무엇이 될까? 이 return이 문제의 discounted, continuing 공식과 어떻게 다른가?
일단 각 타임스텝마다 reward는 0을 받을 것이고 에피소드의 마지막에 실패했을 때 -1을 받을 텐데 여기에도 감가율은 적용돼 -1을 온전히 받지는 않을 것임. 그리고 terminal state가 reward가 -1일때라면 -1을 reward로 받고 다음 episode를 진행하겠지.
근대 continuing을 생각해보면 reward를 -1을 받는게 한번이 아니지 않을까. 감가율은 적용되지만 reward로 받는 -1이 계속 누적될 것 같음.
Exercise 3.7 미로를 탐험하는 로봇을 설계한다고 상상해보자. reward를 탈출하면 +1, 그 밖의 타임스텝에는 0을 reward로 준다. 문제는 자연스럽게 episode로 나눌 수 있고 목표는 expected total reward(3.7)를 최대화하는 것이다. 에이전트를 한 동안 학습시킨 후에 에이전트가 미로를 탈출하는데 발전이 없음을 알 수 있다. 무엇이 잘못인가? 에이전트가 목표를 달성할 수 있게 효율적으로 학습시킬 수 있을까?
식(3.7)이 뭐였는지 갖고 와 보자

이 식을 보면 문제가 감가율이 적용되지 않았음을 알 수 있음. reward에 감가율을 적용시키면 빠르게 탈출할 수록 감가율이 덜 곱해진 reward를 받게 될 것이고 에이전트의 expected reward는 높아질 것이라고 예측 가능.
그렇다면 감가율을 적용시킨 새로운 식을 등장시키자!

Exercise 3.8 \( \gamma=0.5 \), 받은 reward의 sequence를 \( {R}_{1}=-1,{R}_{2}=2,{R}_{3}=6, {R}_{4}=3, {R}_{5}=2 \)라 하고 \( T=5 \)라 하자. \( {G}_{0}, {G}_{1}, ..., {G}_{5} \)는 무엇인가?(힌트: backward로 생각해보자)
Exercise 3.7에서 해답으로 제시한 식을 이용해 expected reward의 값을 계산해보자

그러면 다음과 같이 쓸 수 있는데 T=5까지 이므로 \( {G}_{5} \)의 값은 솔직히 reward를 0이라고 준것도 아니고 이 값을 정의할 수 있는지 조차 잘 모르겠음... 하여튼 간에 식을 저렇게 써놓고 보니 왜 backward로 생각해보자라고 힌트를 줬는지 알 수 있는 부분

그리고 다음과 같이 \( {G}_{t} \)와 다음 return값인 \( {G}_{t+1} \)의 관계식으로 쓸 수 있음. 그러면 계산이 더 쉬워짐. 이렇게 바꾸고 계산을 하면

최종적으로 다음과 같은 값을 얻음 \( {G}_{0}=2, {G}_{1}=6, {G}_{2}=8, {G}_{3}=4, {G}_{4}=2, {G}_{5}=??? \)
Exercise 3.9 \( \gamma=0.9 \)이고 무한 sequence 7s에 따라오는 reward sequence의 \( {R}_{1}=2 \)이면(reward sequence is \( {R}_{1}=2 \) followed by an infinite sequence of 7s.) \( {G}_{1} \)과 \( {G}_{0} \)는 무엇인가?
원서를 보면서 느끼는건 내가 번역을 제대로 한건지도 모르겠고 그렇다고 번역기가 제대로 돌아갔는지도 모르겠다는 것... 하여튼 저렇게 해석을 하고 문제를 풀어보자
근데 7s의 infinite sequence가 뭔지는 모르겠는데 앞에서 이런식을 유도했었음. 그래서 나온 \( {G}_{t} \)와 \( {G}_{t+1} \)의 관계식.

여기서 \( {G}_{t}= {G}_{0} \)이고 \( {G}_{t+1}={G}_{1} \)이 되겠지 그래서 다음과 같이 구할 수 있음

짜잔
Exercise 3.10 공식(3.10)을 증명하라.
다시 불러온 (3.10)을 보자

그리고 이걸 증명하자. 이 문제를 풀때는 무한급수의 합에 대한 지식이 필요한데 까먹어서 다시 찾아봤음
일단 반환값에 대한 식을 다시 써보자

근데 조건을 보면 모든 reward=+1일때 정의 했음을 알 수 있으므로 reward=1임

그리고 무한급수의 합이 무엇인지 증명하자. 일단 \( \gamma \)를 곱해주고

이 둘을 빼줌. 그래서 아래와 같이 나왔음.

여기서 \( {G}_{t} \)끼리 묶고 계산을 함. \( \gamma < 1 \)이기 때문에 0으로 수렴을 해 결국 공식(3.10)과 같이 나옴

Reference : Reinforcement Learning : An Introduction
'강화학습 > Reinforcement Learning An Introduction' 카테고리의 다른 글
| Reinforcement Learning 책 읽고 공부하기(3-3) (0) | 2020.03.12 |
|---|---|
| Reinforcement Learning 책 읽고 공부하기(3-2) (0) | 2020.03.09 |
| Reinforcement Learning 책 읽고 공부하기(3) (0) | 2020.03.01 |
| Reinforcement Learning 책 읽고 공부하기(2-5, Exercise) (1) | 2020.02.24 |
| Reinforcement Learning 책 읽고 공부하기(2-4, Exercise) (0) | 2020.02.21 |