sutton 교수의 Reinforcement Learning An Introduction을 읽고 공부하기
3.5 Policies and Value Functions
거의 모든 강화학습 알고리즘들은 에이전트가 해당 state에 있는게 얼마나 좋은지 계산하는 value function(state의 function 또는 state-action쌍)을 포함한다.(또는 주어진 state에서 주어진 action을 하는게 얼마나 좋은지). "얼마나 좋은지"는 미래 reward의 기대값, 즉 expected return으로 정의한다. 당연하게도 미래에 받을 것이라 기대하는 reward는 에이전트가 어떤 action을 할지에 달려있다. 따라서 value function은 어떻게 policy라 부르는 어떻게 acting해야하는지에 의해 정의된다.
공시적으로 policy는 state에서 action을 선택하는 확률이다. 에이전트가 time t에서 policy \( \pi \)를 따르면 \( \pi\left( a|s \right) \)로 나타내고 이는 \( {S}_{t}=s \)에서 \( {A}_{t}=a \)를 할 확률이다. 강화학습 방법은 에이전트의 policy가 경험에 의해 어떻게 바뀌는지 구체화한다.
Policy \( \pi \)의 영향 아래 있는 state의 value function은 \( v_{\pi} \left( s \right) \)로 표시한다. 이는 s에서 시작해 \( \pi \)를 따랐을때의 expected return이다. MDP로 \( v_{\pi} \)는 다음과 같이 공식화한다.
$$ v_{\pi} \left( s \right) \doteq E_{\pi} \left[ {G}_{t} | {S}_{t} = s \right] = E_{\pi} \left[ \sum_{k=0}^{\infty} \gamma^{k} {R}_{t+k+1} | {S}_{t}=s \right], \textrm{ for all} \,\, s \in S $$
\( E_{\pi} \left[ \cdot \right] \)은 에이전트가 policy \( \pi \)를 따랐을때 주어지는 랜덤 변수의 expected value이다. terminal state의 value는 항상 0이다. \( {v}_{\pi} \) 함수를 policy \( \pi \)의 state-value function이라 한다.
이와 비슷하게 policy \( \pi \)하의 state s에서 action a를 선택했을때의 value를 \( {q}_{\pi} \left( s,a \right) \)라한다. 이는 policy \( \pi \)를 따르는 state s가 action a를 선택했을때 expected return이다.
$$ {q}_{\pi} \left( s,a \right) \doteq {E}_{\pi} \left[ {G}_{t} | {S}_{t}=s, {A}_{t}=a \right] = {E}_{\pi} \left[ \sum_{k=0}^{\infty} \gamma^{k} {R}_{t+k+1} | {S}_{t}=s, {A}_{t}=a \right] $$
\( {q}_{\pi} \)를 policy \( \pi \)의 action-value function이라 부른다.
value function \( {v}_{\pi} \)와 \( {q}_{\pi} \)는 경험을 통해 계산할 수 있다. 예를 들어 에이전트가 policy \( \pi \)를 따르며 각 state를 만날 때마다 평균을 유지해 놓으면 state의 실제 return은 state의 value인 \( {v}_{\pi} \left( s \right) \)에 수렴할 것이다. 각 state마다 각 action의 평균을 유지해놓으면 이것도 비슷하게 action value \( {q}_{\pi} \left( s,a \right) \)에 수렴한다. 우리는 이런 종류의 계산방법을 Monte Carlo 방법이라 부른다. 왜냐하면 실제로 받은 return의 많은 샘플들의 평균을 포함하고 있기 때문이다.
강화학습과 다이내믹 프로그래밍을 통해 사용되는 value function의 근본적인 특성은 return을 계산하기 위해 이미 세웠던 것(3.9)과 유사한 재귀적인 관계를 만족한다. 어떠한 policy \( \pi \)와 어떠한 state s에서도 아래의 s의 value와 그 가능한 state들 사이의 구성조건은 아래와 같다.

action a는 집합 \( A \left( s \right) \)에서 나온 것이고 next state s'은 집합 \( S \)(또는 episodic 문제의 경우에서는 \( S^{+} \)), 그리고 reward r은 집합 R에서 나온 것이다. 마지막 등호를 보면 s'의 value와 r의 value로 나온 두개의 sum을 가능한 value로 하나의 sum을 이용해 표시했다. 공식을 단순화 시키기 위해 이런 병합을 사용했다. 이건 실제로 세변수 a, s', r의 모든 값에 대한 합계이다. 각 세변수에 대해 그 확률(\( \pi \left( a|s \right) p \left( s', r | s, a \right) \))을 계산한다. 이는 확률에 따라 가중치를 부여해 모든 가능성에 대해 합산해 expected value를 얻는다.
방정식 (3.14)는 \( {v}_{\pi} \)의 벨만 방정식이다. 이는 state와 다음 state간의 관계를 말해준다. 아래의 다이어그램은 state와 가능한 다음 state을 보여준다. 흰 원은 state를 검은 원은 state-action 쌍을 나타낸다. 최상단의 루트 노드인 state s에서시작해 에이전트는 policy \(\pi \)에 따라 다이어그램에서 보이는 세가지 action을 선택할 수 있다. 각 쌍에서 환경은 function p에 의해 주어진 dynamics에 의해 다음 state s'과 그 사이 reward r에 대응한다. 벨만 방정식(3.14)은 일어날 각 확률 p에 가중치를 둔 평균이다. start state의 value는 (discouned)된 expected next value에 reward를 더한 것과 같다.
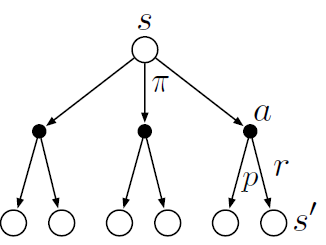
value function \( {v}_{\pi} \)는 벨만 방정식의 유일한 해이다. 위와 같은 다이어그램을 백업 다이어그램이라고 부른다. 왜냐하면 다이어그램의 관계는 강화학습의 심장인 backup operation에 기반을 두고 있기 때문이다. 이 operation은 value information을 state(또는 state-action 쌍)에서 그 하위의 state(또는 state-action 쌍)에 전송한다(back). transition 그래프랑은 다른데 backup 다이어그램의 state node는 반드시 개별 state를 의미하는 것은 아니다. 예를 들어 state는 그 자신의 다음 state일 수도 있다.
value function과 policy에 대해 설명해주는 섹션
state나 action의 value function이란 그 state 또는 action에 있는게 얼마나 좋은지를 계산한 것임. 그리고 value function은 reward들의 기대값인 expected return으로 정의함. 그리고 이 reward란건 에이전트가 어떤 action을 하는지에 달려있으므로 어떤 action을 선택하는지를 정하는 policy도 고려를 해야함.
Example 3.5: Gridworld
그림 3.2의 왼쪽은 단순 유한 MDP로 사각형의 그리드월드를 표현한 것이다. 그리드의 셀들은 환경의 state에 대응한다. 각 셀들은 상,하,좌,우 네가지 액션이 가능하고 deterministically하게 움직인다. 그리드를 벗어나는 action은 셀의 위치가 변하지 않고 reward는 -1이다. 다른 action들의 reward는 0이다. state A에서 모든 4개의 action은 reward가 +10이고 에이전트는 A'으로 간다. state B에서 모든 action들의 reward는 +5이고 에이전트는 B'으로 간다.
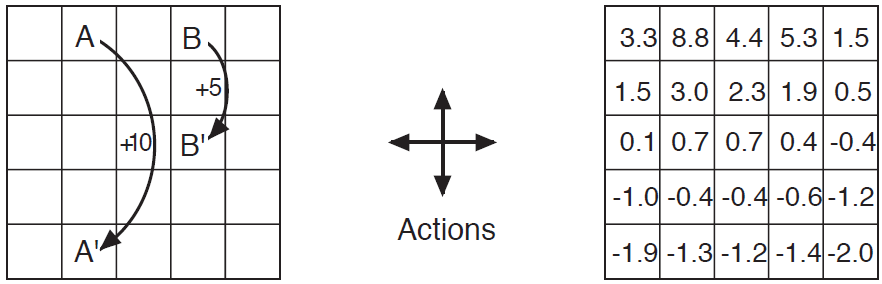
에이전트가 모든 4개의 action들을 같은 확률로 선택한다고 가정하자. 그림 3.2(오른쪽)은 이 policy에 \( \gamma=0.9 \)를 적용한 value function(\( {v}_{\pi} \))을 보여준다. value function들은 부등식(3.14)을 계산한 것이다. 하단 가장자리가 음의 값인 것을 알 수 있는데 이는 무작위 policy하에서 그리드의 가장자리를 넘어갈 확률이 높음을 의미한다. state A가 이 policy에서 가장 좋은 state이지만 expected return은 10보다 작다. 왜냐하면 이제는 즉각적인 reward이고 A에서 에이전트는 A'(그리드의 가장자리)으로 가기 때문이다. state B는 반면에 value가 5보다 큰데 에이전트는 B에서 B'으로 가기 때문이다. B'에서 가장자리까지 갈 예상되는 penalty는 A 또는 B로 넘어갈 수 있는 예상되는 이득에 의해 보정된다.
그리드월드예제를 통해 가치함수에 대해서 알려주고 있음. 밑의 가장자리에서는 value가 꽤 낮은 것을 볼 수 있음.
A -> A'으로 갈때는 밑의 A'이 바로 경계선을 넘어버리면 (-)를 reward로 받기 때문에 즉각적인 reward인 10보다 낮은 값을 갖고 B -> B'으로 갈때는 밑의 B'이 경계선을 넘을 확률이 더 낮고 다른 A 또는 다시 B로 갈 수도 있으니 reward +5보다 높은 value function을 갖는 것을 알 수 있음.
Example 3.6: Golf
강화학습문제로 골프하는 것을 공식화해보자. 공이 홀에 들어가기 전까지 각 타수당 -1의 reward를 얻는다. state는 공의 위치이다. state의 value는 공의 위치에서 홀까지 타수의 (-)값이다. 여기서 action은 putter 또는 driver 중 어떤 클럽으로 공을 칠 것인지 선택하는 것이다. 그림 3.3의 위쪽은 putter를 사용했을 때 policy의 가능한 state-value function(\( {v}_{putt} \left( s \right) \))이다. terminal state인 in-the-hole의 value는 0이다. 어디에서든지 green은 putt을 할 수 있다고 가정한다. 이 state들의 value는 -1이다. green 밖에서는 putting으로 홀에 도달할 수 없고 value는 더 크다. 만약 putting으로 state에서 green으로 도달하면 state는 반드시 green보다 하나 낮은 값인 -2여야 한다.

단순하게 하기 위해 putt은 아주 정확하지만 제한된 범위를 가진다고 하자. 이는 그림에서 -2로 명명된 날카로운 경계를 준다. 이 라인과 green 사이의 모든 장소들은 홀에 들어가기 위해 정확하게 2타가 필요하다. 비슷하게 어떤 장소던지 -2의 putting 범위를 가지는 경계의 value는 반드시 -3이다. 그리고 모든 경계는 그림과 같다. putting은 모래에서 밖으로 나오게 하진 못하므로 이때 value는 \( -\infty \)다. 전반적으로 putting으로 tee를 홀로 가져가려면 6타가 필요하다.
3.6 Optimal Policies and Optimal Value Functions
강화학습 문제를 푼다는 것은 대략 긴 학습시간에서 많은 reward를 받게하는 policy를 찾는 것이다. 유한 MDP에서 다음과 같은 방법으로 optimal policy를 정확하게 정의한다. value function은 policy에 대한 부분적인 순서를 정의한다. policy \(\pi \)는 모든 state에 대한 expected return값이 polciy \( \pi^{'} \)보다 크거나 같으면 \( \pi \geq \pi^{'} \)이고 \( {v}_{\pi} \left( s\right) \geq {v}_{\pi'} \left(s \right) \)로 나타낸다. 항상 적어도 하나의 policy가 다른 모든 policy보다 같거나 크다. 이게 optimal policy다. 비록 하나보다 더 많이 있을지라도 모든 optimal policy를 \( {\pi}_{*} \)로 표시한다. 그것들은 optimal state-value funciton이라 불리는 같은 state-value function을 공유한다. \( {v}_{*} \)로 표시하고 아래와 같이 정의한다.
$$ {v}_{*} \left( s \right) \doteq \underset{\pi}{max} \,{v}_{\pi} \left( s \right) \textrm{for all} \,\,\, s \in S $$
Optmal policy는 또한 \( {q}_{*} \)로 표시되는 같은 optimal action-value function를 공유하고 다음와 같이 정의한다.
$$ {q}_{*} \left( s,a \right) \doteq \underset{\pi}{max} \, {q}_{\pi} \left( s,a \right) \textrm{for all} \,\,\, s \in S, a \in A\left( s \right) $$
State-action 쌍(s,a)에서 이 함수는 optimal policy를 따랐을 때 state s에서 action a를 선택했을 때 expected return을 준다. 그래서 \( {q}_{*} \)는 \( {v}_{*} \)를 이용해 다음과 같이 쓴다.
$$ {q}_{*} \left( s,a \right) = E\left[ {R}_{t+1} + \gamma {v}_{*} \left( {S}_{t+1} \right) | {S}_{t}=s,{A}_{t}=a \right] $$
왜냐하면 \( {v}_{*} \)는 policy에 의해 value function이기 때문에, 반드시 state value(3.14)의 벨만 방정식의 self-consistency 조건을 만족해야한다. 왜냐하면 이는 optimal value function이기 때문에 \( {v}_{*} \)의 consistency 조건을 어떠한 구체적 policy를 참고하지 않고 특별한 형태로 쓸 수 있다. 이게 \( {v}_{*} \)를 위한 벨만 방정식 또는 Bellman optimality equation(벨만 최적 방정식)이라 부른다. 직관적으로 벨만최적방정식은 optimal policy하의 state의 value가 반드시 state가 가진 최선의 action의 expected return과 같다는 사실을 표현한다.

마지막의 두 방정식들은 \( {v}_{*} \)로 나타낸 벨만 최적 방정식의 두가지 형태이다. \( {q}_{*} \)로 나타낸 벨만 쵲적 방정식은 아래와 같다.

밑의 그림에 나온 backup 다이어그램은 \( {v}_{*} \)와 \( {q}_{*} \)의 벨만 최적 방정식의 미래 state와 action들을 그래픽으로 팽창시킨 것이다. 이는 앞에 나온 backup 다이어그램에서 에이전트의 action 선택 부분에 호가 추가되어 일부 policy에 따라 expected value보다 최대값이 선택된다는 것을 빼면 앞의 \( {v}_{\pi} \)와 \( {q}_{\pi} \)의 backup 다이어그램과 동일하다. 왼쪽의 backup 다이어그램은 벨만 최적 방정식을 그래픽으로 나타낸 것이고(3.19) 오른쪽은 (3.20)을 나타낸 것이다.

유한 MDP에서 \( {v}_{*} \)로 나타낸 벨만 최적 방정식(3.19)는 유일한 해결책을 가지고 있다. 벨만 최적 방정식은 실제로 각 state에 대한 하나의 방정식 시스템으로 n개의 state가 있으면 n개의 미지수에 n개의 방정식이 있다. 만약 환경의 dynamics p를 알고 있다면 원칙적으로 비선형 방정식을 풀기 위한 다양한 방법 중 하나를 선택해 \( {v}_{*} \)에 대한 방정식 시스템을 풀 수 있다.
일단 \( {v}_{*} \)가 있으면 optimal policy를 결정하기가 상대적으로 쉽다. 각 state s에서 벨만 최적 방정식으로 얻을 수 있는 최대값은 하나 또는 더 많은 action들이 있을 수 있다. 이러한 action들에만 0이 아닌 확률을 할당하는게 optimal policy다. 이것을 one-step search로 생각할 수 있다. 만약 optimal value function인 \( {v}_{*} \)를 가지고 있다면 one-step search 후 나타나는 최선의 action은 optimal action일 것이다. 이말은 곧 optimal evaluation function인 \( {v}_{*} \)와 관련해 greedy policy가 optimal policy라는 것이다. greedy라는 용어는 탐색이나 결정하는데 오직 눈 앞의 이득만을 생각하는 것이다. 결과적으로 이는 action을 policy로 action을 선택할때 오직 단기 결과만 고려함을 의미한다. \( {v}_{*} \)를 사용하여 optimal expected long-term return은 각 state에서 가능한 지역적이고 즉각적인 양으로 바뀐다. 그래서 one-step-ahead search는 장기적으로 optimal action들을 만들어 낸다.
\( {q}_{*} \)를 가지고 있으면 optimal action을 선택하는 것을 더 쉽게 만들어준다. \( {q}_{*} \)가 있으면 에이전트는 one-step-ahead search를 할 필요가 없다. 어떠한 state s에서든 \( {q}_{*} \left( s,a \right) \)를 최대화할 수 있는 어떤 action을 쉽게 찾을 수 있다. action-value 함수는 모든 one-step-ahead search의 결과를 효과적으로 cache한다(저장 or 고속으로 처리). 이는 각 state-action쌍에 대해 지역적이고 즉각적인 값으로 optimal expected long-term return을 value로 준다. optimal action-value function은 가능한 다음 state와 그 value를 뭔지 몰라도 optimal action을 선택할 수 있게 해준다. 이말은 환경의 dynamics를 몰라도 optimal action을 선택할 수 있다는 말이다.
강화학습 문제를 푼다는 것은 reward를 제일 받이 많게 해주는 policy를 찾는 것임. 그리고 가장 큰 value function을 주는 policy가 optimal policy로 \( {\pi}_{*} \)로 표시함. state와 action에 대해서 optimal policy를 적용한 optimal state value는 \( {v}_{*} \left( s \right) \)이고 optimal action value는 \( {q}_{*} \left( s,a \right) \)로 표시함.
(3.17)의 경우 optimal policy를 따르고 state s에서 action a를 선택했을 때 expected return인데 이걸 \( {v}_{*} \)로 표시한 것임. 그리고 (3.19)를 벨만 최적 방정식이라하는데 벨만 최적 방정식은 optimal policy하의 state에서 best action을 선택했을 때의 expected return과 같음.
Example 3.7: Optimal Vlalue Functions for Golf
그림 3.3의 아래쪽부분은 가능한 optimal action-value function인 \( {q}_{*} \left(s, driver \right) \)를 보여준다.
Example 3.8: Solving the Gridworld
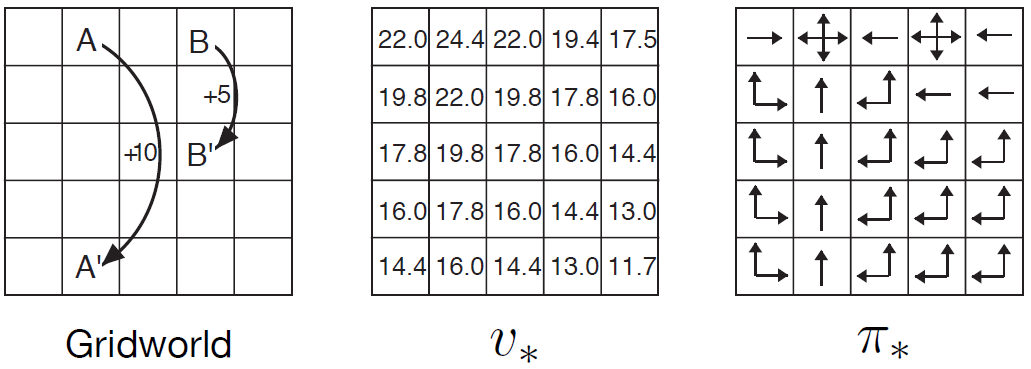
Example 3.5와 그림3.5의 왼쪽과 같은 간단한 그리드월드 예제의 \( {v}_{*} \) 벨만 방정식을 푼다고 생각해보자. state A는 state A'으로 전이되며 +10의 reward를 받고 B는 B'으로 전이되며 +5의 reward를 받는다. 그림3.5의 가운데는 optimal value function을 보여준다. 그리고 그림 3.5의 오른쪽은 이에 대응하는 optimal policy를 보여준다. 셀 안에 여러개의 화살표가 있는 것은 모든 action들이 optimal이라는 뜻이다.
Example 3.9: Bellman Optimality Equations for the Recycling Robot
(3.19)를 사용해 재활용 로봇예제에 명확한 벨만 최적 방정식을 줄 수 있다. 더 간결하게 만들기 위해 state인 high, low action인 search, wait, recharge를 각각 h, l, s, w 그리고 re로 축약한다. state가 오직 두 개이기때문에 벨만 최적 방정식도 두개의 방정식을 가진다. \( {v}_{*} \left(h \right) \)의 방정식은 아래와 같이 쓸 수 있다.

\( {v}_{*} \left( l \right) \)에 대해 동일한 절차를 따르면 아래와 같은 방정식이 산출된다.

\( {r}_{s}, {r}_{w}, \alpha, \beta, \gamma \)(\( 0 \leq \gamma < 1, 0 \leq \alpha, \beta \leq 1 \))에서 어떤 선택을 하든 비선형 방정식인 \( {v}_{*} \left( h \right) \)와 \( {v}_{*} \left( 1 \right) \)를 둘 다 동시에 만족하는 하나의 쌍이다.
벨만 최적 방정식을 명시적으로 해결하면 optimal policy를 찾는 한가지 경로를 알 수 있고 강화학습 문제를 풀 수 있다. 하지만 이 해결책은 거의 유용하지 않다. 이는 철저한 탐색(exhaustive search)과 유사해 모든 가능성을 계속 찾고 그것들이 일어날 가능성과 expected rewards를 계산한다. 이 해결책은 실제로는 거의 사실이 아닌 최소한 세가지 가정에 의존한다. (1) 환경의 dynamics를 정확히 안다. (2) 해결법의 계산을 완전히 할 수 있을정도로 계산자원이 충분하다. 그리고 (3) Markov property. 우리가 관심있어하는 종류의 작업들에 관해 일반적으로 이러한 가정의 다양한 조합이 위반되기 때문에 해결책을 정확하게 구현할 수 없다.(For the kinds of tasks in which we are interested, one is generally not able to implement this solution exactly because various combinations of these assumptions are violated.) 예를 들어 (1)과 (3)의 가정은 backgammon 게임에서 문제가 없을지라도 (2)는 주요한 방해물이다. 왜냐하면 이 게임이 \( 10^{20} \)개의 state들을 가지고 있기 때문이다. 이는 벨만 방정식 (\ {v}_{*} \)를 풀기 위해 오늘날의 가장 빠른 컴퓨터를 사용해도 몇천녀이 걸리고 \( {q}_{*} \)의 참값을 구하는 것도 똑같다. 강화학습에서는 일반적으로 근사 해결법을 정해야 한다.(In reinforcement learning one typically has to settle for approximate solutions.)
벨만 최적 방정식을 대략적으로 해결하는 방법으로 다양한 decision-making 방법을 볼 수 있다. 예를 들어 휴리스틱 탐색 방법은 (3.19)의 오른쪽을 몇번의 깊이까지 확장해 가능성의 "트리"를 형성하는 것으로 볼 수 있다. 그리고 "leaf" 노드의 \( {v}_{*} \)를 근사하기 위해 휴리스틱 evaluation function을 사용한다.(\( A^{*} \)와 같은 휴리스틱 탐색 방법은 거의 항상 episodic case에 기반을 두고 있다.) 다이나믹 프로그래밍 방법은 벨만 최적 방정식과 더 밀접하게 연관되어 있을 수도 있다. 많은 강화학습 방법들은 expected transition에 대한 지식 대신 실제 experienced transition을 사용해 벨만 최적 방정식을 대략적으로 해결하는 것으로 이해할 수 있다. 다음 장에서 다양한 방법을 고려한다.
3.7 Optimality and Approximation
앞에서 optimal value function과 optimal policy를 정의했다. 에이전트는 optimal policy를 잘 학습했지만 실제로 이는 매우 드물다. 우리가 관심있어하는 문제들의 optimal policy들은 오직 엄청난 계산을 통해서 얻어진다. 위에서 논의한 것처럼 우리가 완전하고 정확한 환경의 dynamics의 모델을 알아도 벨만 최적 방정식을 풀어 optimal policy를 단순하게 계산하는 것은 불가능하다. 예를 들어 체스같은 보드 게임들은 사람의 경험에서는 작은 부분이지만 아직 대형 컴퓨터들은 optimal move를 계산하지 못한다. 에이전트가 마주보는 가장 중요한 측면은 주어진 계산량이다. 특히 하나의 타임스텝에서 에이전트가 계산할 수 있는 양이다.
가용할 수 있는 메모리 또한 중요한 제약조건이다. 대용량의 메모리는 value function, policy, model들의 근사를 빌드하기 위해 필요하다. 작은 작업과 유한 state에서는 배열이나 테이블을 사용해 각 state의 근사를 할 수 있다. 이런 방법을 tabular 경우라 부르고 여기에 맞는 방법을 tabular 방법이라 부른다. 하지만 실제로 흥미가 있는 다양한 경우들은 테이블로 표현할 수 있는 것보다 훨신 많은 satte가 존재한다. 이런 경우에서 function들은 반드시 더 간결하게 파라미터화된 function들을 사용해 근사해야한다.
우리의 강화학습에 대한 틀은 우리가 이런 근사치를 정하게 강요한다. 하지만 우리에게 유용한 근사치를 달성할 수 있게 기회를 준다. 예를 들어 optimal behavior를 근사할 때 에이전트가 suboptimal actoin을 선택할 낮은 확률로 직면한 많은 state가 있을 수 있음은 에이전트가 받을 reward에 아주 낮은 영향을 준다.
예를 들어, optimal behavior를 근사할 때, 에이전트가 suboptimal action을 선택하는 것은 에이전트가 받는 reward에 거의 영향을 미치지 않을 정도로 낮은 확률로 에이전트가 직면하는 state가 많을 수 있다.(For example, in approximating optimal behavior, there may be many states that the agent faces with such a low probability that selecting suboptimal actions for them has little impact on the amount of reward the agent receives.) 예를 들어 Tesauro backgammon 플레이어는 전문가와의 게임에서는 절대 일어나지 않을 게임의 상태에 대해서 나쁜 결정을 내릴 수 있는데도 불구하고 예외적인 스킬로 게임한다. 사실 TD-Gammon은 아주 다양한 게임의 상태에서 상당부분 나쁜 결정을 내릴수도 있다. online 강화학습의 특징은 자주 접하지 않는 state에 대해서는 노력을 줄이고 자주 접하는 state에 대해 더 좋은 결정을 내리기 위해 더 많이 노력하는 optimal policy를 근사할 수 있다. 이는 MDP를 대략적으로 해결하기 위한 다른 접근방법들과 강화학습을 구분해주는 중요한 특징이다.
3.8 Summary
이번챕터에서 보여준 강화학습 문제들의 요소들을 요약한다. 강화학습은 goal을 달성하기 위해 환경과 어떻게 상호작용하며 행동을 하는지를 학습하는 것이다. 강화학습 에이전트와 환경은 불연속적인 타임스텝의 순서로 서로 상호작용한다. 이들의 인터페이스의 specification은 특정 task를 정의한다. action은 에이전트에 의한 선택이고, state는 이런 선택을 만들기 위한 기초이다. 그리고 reward는 이런 선택을 평가하기 위한 기초이다. 에이전트에 안에 있는 모든 것들은 에이전트에 의해 완벽하게 알려져 있고 조절할 수 있다. 에이전트 밖의 모든 것들은 완전하게 조절할 수 없고 완전히 알 수도 있고 모를 수도 있다. Policy는 state의 함수로서 에이전트가 action을 선택하는 확률론적인 법칙이다(stochastic rule). 에이전트의 목표는 이런 시간에 거쳐서 받을 reward들을 최대화하는 것이다.
위에서 설명한 강화학습의 설정은 transition probability인 MDP로 아주 잘 정의될 수 있다. 유한 MDP는 한정된 state, action, reward set을 지닌 MDP이다. 강화학습의 많은 현재 이론들은 유한 MDP로 제한되어 있지만, 그 방법과 아이디어는 보다 일반적으로 적용된다.
Return은 에이전트가 (expected value에서)최대화하려고 하는 future reward의 함수이다. Return은 task의 특성과 delayed reward를 discount할지에 따라 몇몇의 다른 정의가 있다. undiscounted formulation은 episodic task에 적합하다. discounted formulation은 continuing task, 즉 상호작용이 자연스럽게 episode로 떨어지지 않고 제한없이 지속되는 task에 적하다. 우리는 두 종류의 task를 하나의 방정식이 epsiodic과 continuing의 경우에 모두 적용할 수 있게 정의하려고 노력했다.
Policy의 value function은 에이전트가 policy를 사용할 경우 각 state 또는 state-action 쌍, 즉 해당 state로부터 expected return 또는 state-action 쌍에 할당된다. optimal value function은 각 state 또는 state-action 쌍에 할당되며 어떤 policy에서 달성가능한 가장 큰 expected return이다. value functino이 optimal한 policy는 optimal policy다. 반면에 state와 state-action 쌍의 optimal value function들은 주어진 MDP에 고유한 것이지만, 여러가지 optimal policy가 있을 수 있다. optimal value function에 대해 greedy한 모든 policy는 optimal 여기서 policy여야 한다. 벨만 최적 방정식은 optimal value function을 반드시 만족해야하며, 원칙적으로 optimal value function에 대해 해결할 수 있어야하는 특수한 일관성 조건이며 여기서 optimal policy조건을 상대적인 용이성으로 결정할 수 있다.
강화학습 문제는 최초에 에이전트에게 이용가능한 지식의 수준에 대한 가정에 따라 다양한 다른 방법으로 제기할 수 있다. complete knowledge문제에서, 에이전트는 완전하고 정확한 환경의 dynamics에 대한 모델을 가지고 있다. 만약 환경이 MDP라면, 그런 모델은 완전한 4개의 아규먼트를 가진 dynamics function p(3.2)로 구성된다. incomplete knowledege 문제에서는, 완전하고 완벽한 환경의 모델은 불가능하다.
만약 에이전트가 완전하고 정확한 환경의 모델을 가지고 있어도, 에이전트는 일반적으로 그것을 모두 사용하기 위해 타임스텝마다 충분한 계산을 할 수는 없다. 메모리 가용량 또한 중요한 제약조건이기 때문이다. 메모리는 value function, policy, model의 정확한 근사치를 구축하기 위해 메모리가 필요할 수도 있다. 실제적으로 흥미를 끄는 대부분의 경우 테이블로 표현할 수 있는 것보다 더 많은 state가 존재하며, 반드시 근사치가 만들어져야 한다.
optimlity의 명확한 개념은 우리가 이책에서 설명하는 학습에 대한 접근을 잘 체계화하고 다양한 학습 알고리즘의 이론적인 특성들을 이해할 수 있는 방법을 제공한다. 하지만 강화학습 에이전트는 단지 다양한 정도에서 근사할 수 있는 것이 이상적이다. 강화학습에서 우리는 optimal한 해결책을 찾을 수 없지만 반드시 어떠한 방법으로 근사하는 경우에 경우에 대해 매우 많은 관심이 있다.
Reference : Reinforcement Learning : An Introduction
'강화학습 > Reinforcement Learning An Introduction' 카테고리의 다른 글
| Reinforcement Learning 책 읽고 공부하기(4) (0) | 2020.05.22 |
|---|---|
| Reinforcement Learning 책 읽고 공부하기(3, Exercise2) (0) | 2020.03.12 |
| Reinforcement Learning 책 읽고 공부하기(3-2) (0) | 2020.03.09 |
| Reinforcement Learning 책 읽고 공부하기(3, Exercise) (2) | 2020.03.09 |
| Reinforcement Learning 책 읽고 공부하기(3) (0) | 2020.03.01 |