sutton 교수의 Reinforcement Learning An Introduction을 읽고 공부하기
Dynamic Programming
Dynamic programming(DP)는 MDP로 환경의 완벽한 모델이 주어졌을 때 optimal policy를 계산하기 위한 알고리즘들의 collection이다. 전통적인 DP 알고리즘들은 완벽한 모델의 대한 가정과 엄청난 계산량 때문에 강화학습에서의 활용성은 제한되었다. 하지만 이론적으로는 여전히 중요하다. DP는 이 책에 나머지 부분에 설명되는 방법들을 이해하기 위한 필수적인 기초를 제공해준다. 사실 이러한 모든 방법들은 계산을 덜하고 환경에 대한 완벽한 정보없이, DP와 동일한 효과를 달성하기 위한 시도들이라고 볼 수도 있다.
우리는 보통 환경을 finite MDP라고 가정한다. 그 말은 state, action, reward 집합들이 한정되어 있다는 뜻이고 dynamics가 확률의 집합인 \(p\left( s',r|s,a \right) \)로 주어진다는 말이다. DP 아이디어가 continuous state와 action 문제에도 적용가능하긴 하지만, 정확한 solution은 특별한 경우에 가능하다. continuous state와 action의 task를 위한 근사 solution을 얻기 위한 흔한방법은 state와 action space를 quantize하고 finite-state DP 방법을 적용하는 것이다. 우리가 Part II에서 발견한 방법은 continuous 문제에 적용가능하고 이런 approach에 중요한 확장이다.
DP의 핵삼 아이디어(그리고 강화학습의 일반적인 아이디어)는 좋은 policy를 찾기 위해 value function을 사용하는 것이다. 이 챕터에서 우리는 Chapter 3에 정의된 value function을 계산하는데 DP가 어떻게 사용되는지 볼 것이다. 나중에 얘기할 것이지만 우리는 벨만 최적 방정식을 만족하는 optiaml value function(\({v}_{*} \) 또는 \({q}_{*} \))을 찾으면 optimal policy들은 쉽게 얻을 수 있다.

우리가 봤던 것처럼 DP알고리즘은 이와 같은 벨만방정식을 대입, 즉 원하는 value function의 근사치를 개선하기 위한 업데이트 규칙을 변환하여 얻는다.
4.1 Policy Evaluation(Prediction)
첫번째로 임의의 policy \(\pi \)에서 state-value function \({v}_{\pi} \)를 어떻게 계산해야하는지 생각해본다. 이는 DP에서 policy evaluation이라고 부른다. 우리는 또한 이 문제를 prediction problem이라 부른다. Chapter 3에서의 식을 다시 불러와 보자.

\( \pi\left(a|s \right) \)는 policy \(\pi \)하에서 state s에서 action a를 선택할 확률이고, 그리고 expectation의 \( \pi \)는 policy \( \pi \)를 따르고 있음을 말한다. policy \(\pi \)하에 모든 state에서 \(\gamma \)<1 또는 eventual termination이 보장되는 한 \( {v}_{\[pi} \)의 존재와 고유성은 보장된다.(...?)
만약 환경의 dynamics를 완전히 알고 있다면 (4.4)는 \( |S| \)가 미지수인 \(|S| \)의 동시 선형 방정식이다. 원칙적으로 이 해결책은 간단하고, 지루하지만 계산적이다. 우리의 목적에 의해 iterative solution방법이 제일 적합하다. state의 근사 value function들 \({v}_{0}, {v}_{1}, {v}_{2}, ... \)의 sequence는 실수에 매핑된다고 생각하자. 초기 근사치 \({v}_{0} \)는 임의로 선택된다.(terminal state는 반드시 0이어야 한다는 것을 제외하고) 그리고 각각의 그 후에 나오는 근사치들은 아래의 업데이트 식을 사용해 (4.4) \( {v}_{\pi} \)의 벨만 방정식을 사용해 얻는다.
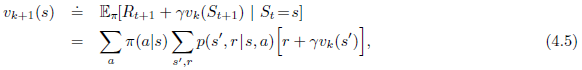
모든 state s에 대해서 \( {v}_{k}={v}_{\pi} \)는 이 업데이트 식에서는 고정된 point다. 왜냐하면 \({v}_{\pi} \)의 벨만방정식은 이 경우 equality를 보장한다. 정말로 \( \left\{ {v}_{k} \right\} \)의 sequence는 \({v}_{\pi} \)의 존재를 보장해주는 같은 조건하에서 \( k \rightarrow \infty \)로 가면 \( {v}_{\pi} \)로 수렴함을 보여준다. 이 알고리즘을 iterative policy evaluation이라 부른다.
\( {v}_{k} \)에서 \( {v}_{k+1} \)인 각 연속 근사치를 생성하기 위해 iterative policy evaluation은 각 state s에 동일한 계산을 적용한다. 이는 evaluate하는 policy에 따라 가능한 모든 one-step transition과 함께, state s의 후속 value에서 얻은 새로운 value와 expected immediate reward로 대체한다. 우리는 이런 연산을 expected update라 한다. iterative policy evaluation의 각 iteration은 value function \({v}_{k+1} \)의 새로운 근사치를 생성해 모든 state의 value를 업데이트한다. state인지 state-action을 업데이트하는지는 후속 state에서 측정된 value를 결합하는 정확한 방법에 따라 몇가지 다른 종류의 expected update가 있다. DP 알고리즘에서 모든 업데이트 완료는 expected update라고 부르는데 왜냐하면 sample next state 대신 가능한 모든 next state의 expectation에 기초를 두고 있기 때문이다. 업데이트의 특성은 위에 보이는 것같은 방정식으로 표현할 수도 있고, Chapter 3에 나온것처럼 백업 다이어그램으로 할 수도 있다. 예를 들어, 백업다이어그램에서 iterative policy evaluation을 사용해 expected update를 하는 것은 chapter 3의 그림 3.4와 같다.
(4.5)와 같은 iterative policy evaluation을 구현하기 위한 sequentail computer program을 작성하려면, old value를 위한\({v}_{k}\left( s\right), \)와 새로운 value를 위한 \({v}_{k+1}\left(s \right) \)의 배열을 두개 써야한다. 배열을 두개를 사용하면 old value가 변할 일 없이 하나하나씩 새로운 value를 변화시킬 수 있다. 당연하게도 하나의 배열을 사용하고 "적재", 즉 각 새로운 value가 즉시 이전 valueㄹ를 덮어쓰면서 업데이트하는 것이 더 쉽다. 근데 state가 업데이트 되는 순서에 의존하기 때문에 때때로 새로운 value들이 (4.5)의 오른쪽 편의 old value들을 대신해 사용된다. 이런 적재 알고리즘 또한 \( {v}_{\pi} \)로 수렴한다. 사실 이는 예상하겠지만 배열이 두개일때보다 더 빠르게 수렴하는데, 왜냐하면 새로운 데이터를 가능하면 바로 사용하기 때문이다. 우리는 업데이트들이 state space들을 휩쓸고 가는 것으로 생각한다. 탑재 알고리즘에서 sweep 중에 state가 값을 업데이트하는 순서는 수렴 속도에 상당한 영향을 미친다. 우리는 보통 DP 알고리즘을 생각할때 탑재(in-place)버전을 염두에 두고 있다.
interative policy evaluation의 완전한 in-place 버전은 아래의 박스에 수도코드로 나와있다. 여기서 종료를 어떻게 처리해야하는지 주의해야한다. 공식적으로 iterative policy evaluation은 한계 내에서만 수렴되지만, 실제로 이를 충족시키지 못하고 더 짧게 중지된다. 이 수도코드는 각 sweep 후 \({max}_{s \in S} | {v}_{k+1}\left(s \right) - {v}_{k}\left( s\right) | \)의 양을 테스트하고 충분히 작을 때 정지한다.

Example 4.1 4x4 그리드월드를 생각해보자

terminal state가 아닌 state들 S={1, 2, ..., 14}이다. 각 action마다 가지의 action A={up, down, right, left}가 가능하다. action들은 deterministic하게 state transition을 하는데 그리드의 밖으로 나가는 actoin의 state는 바뀌지 않는다. 예를 들어 \( p\left(6, -1 | 5, right \right)=1 \), \( p\left( 7, -1|7, right \right)=1 \) 와 같이 항상 1이다. undiscounted, episodic task이고 모든 transition에서 terminal state에 도달하기 전까지 항상 reward는 -1이다. terminal state는 그림에서 검은색 사각형이다. 모든 state s, s'의 action a에서 expected reward function은 \(r\left(s,a,s' \right)=-1 \)로 표현할 수 있다. 에이전트가 action을 선택할 확률이 모드 동일한 랜덤 policy라고 생각하자. Figure r.1의 왼쪽에서 value function \( \left\{ {v}_{k} \right\} \)의 sequence는 iterative policy evaluation에 의해 계산된다. 최종 추정치는 사실상 \( {v}_{\pi} \)이며, 이 경우 각 state에 대해 해당 state에서 종료까지 예상되는 단계수를 음수로 알 수 있다.
4.2 Policy Improvement
우리가 policy를 위한 value function을 계산하는 것은 더 나은 policy를 찾기 위함이다. 어떠한 임의의 deterministic policy \(\pi \)에 대해 value function \({v}_{\pi} \)를 결정했다고 하자. 어떤 state s에서 우리는 action a\(\neq \pi \left(s \right) \)의 policy를 deterministic하게 선택하도록 policy를 바꿔야하는지 알고싶다. 우리는 현재 policy를 따를 때 state s의 value function \({v}_{\pi}\left(s \right) \)이 얼마나 좋은지는 알고 있지만 새로운 policy로 바꾸는게 더 좋은까? 아니면 더 나쁠까?에 대해서는 모른다. 이 질문에 대답하는 한가지 방법은 state s에서 action a를 선택한 후 기존 policy \(\pi \)를 따르는 것을 고려하는 것이다. 이럴 경우 value는 다음과 같다.

여기서 중요한 표준은 \( {v}_{\pi}\left(s \right)\)보다 크거나 작은지의 여부이다. 만약 더 크다면 항상 \(\pi \)를 따르는 것보다 state s 에서 action a를 한번 선택하고 그 후에 \(\pi \)를 따르는 것이 더 낫다면 ,satte s를 만날 때마다 aciotn a를 선택하는 것이 더 낫고, 실제로 새로운 정책이 전반적으로 더 나을 것이라고 기대할 것이다.
항상 PI를 따르는 것보다 S에서 A를 한 번 선택하고 그 후에 PI를 따르는 것이 더 낫다면, S를 만날 때마다 A를 선택하는 것이 더 낫고, 실제로 새로운 정책이 전반적으로 더 나을 것이라고 기대할 것이다.
이것이 참이라는 것은 policy improvement theorem이라고 하는 일반적인 결과의 특수한 경우이다. \(\pi \)와 \(\pi' \)이 deterministic policy의 어떤 쌍이라고 했을 때 모든 state에 대해서 다음과 같이 성립한다.

그러면 policy \(\pi' \)은 \(\pi \)와 같거나 더 좋다. 그러므로 모든 state s에서 더 좋거나 같은 expected return을 얻는다.

게다가, 어떤 state에서든 (4.7)의 식에서 엄격한 불평등(strict inequality)가 있다면, 그 state는 (4.8)의 식에서도 동일한 엄격한 불평등이 있어야 한다.

그림 4.1은 작은 그리드월드에서 iterative policy evaluation의 수렴을 보여준다. 왼쪽의 열은 random policy(모든 action이 동일)에서 state-value function의 근사값들을 나열한 것이다. 오른쪽 열은 value function 평가값에 대응하는 greedy policy를 나열한 것이다(최대값에 도달한 모든 작업에 대해 화살표가 표시되고 표시된 숫자는 유효숫자 2개로 반올림). 마지막 policy는 random policy에 대한 improvement이다. 다만 이 경우는 세번째 iteration 후의 모든 policy는 optimal이다.
Policy improvement theorem은 우리가 이 섹션의 처음에서 본 두가지 policy에 적용한다. \(\pi' \left( s \right) = a \neq \pi\left(s \right) \)를 제외하고 \( \pi \)와 동일한 origianl deterministic policy \(\pi \) 및 변경된 policy인 \(\pi' \). s 이외의 다른 state의 경우 ,양변이 같기 때문에 (4.7)이 유지된다. 그러므로 \( q_{\pi}\left(s, a \right) > v_{\pi} \left(s \right) \)이면, 변경된 policy가 실제 \( \pi \)보다 낫다.
Policy imporvement 정리의 증명 뒤에 있는 아이디어는 이해하기 쉽다. 식 (4.7)에서부터 시작해보자. 우리는 \( q_{\pi} \)쪽을 식 (4.6)을 이용해 계속 확장하고, \( v_{\pi'} \left(s \right) \)를 얻을 때까지 식 (4.7)에 적용할 것이다.

지금까지 우리는 policy와 그 value function이 주어졌을 때, 어떻게 하면 policy의 변화를 단일 state에서 쉽게 평가할 수 있는지를 봤다. \( q_{\pi} \left( s, a \right) \)에 따라 가장 나아보이는 action을 각 state에서 선택하면서, 모든 state에서 변화를 고려하는 것은 자연스러운 연장선이다. 즉, 다음에서 주어진 새로운 geedy policy인 \( \pi' \)을 고려하면,

\(argmax_{a} \)는 다음과 같은 표현이 최대화하는 a의 값을 나타낸다(with ties broken arbitrarily). Greedy policy는 \( v_{\pi} \)에 따라 단기간(한 스탭을 내다본 후)에서 가장 좋은 action을 선택한다. Greedy policy는 policy improvement 정리(4.7)의 조건에 따르므로, original policy에 버금가는 ,또는 더 낫다는 것을 알 수 있다. original policy의 value function에 대해 greedy하게 origianl policy를 개선하는 새로운 policy를 만드는 과정을 policy improvement라 한다.
새로운 geedy policy인 \( \pi' \)이 old policy인 \( \pi\)보다 낫진 않다고 가정해보자. 그럼 \( v_{\pi} = v_{\pi'} \)이고 식 (4.9)에서 all \( s \in S \)이다.
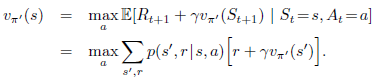
근데 이는 벨만 최적 방정식(Bellman optimality equation)(4.1)과 동일하므로 \( v_{\pi'} \)은 \( v_{*} \)여야 하며, \( \pi \)와 \( \pi' \)은 모두 optimal policy여야 한다. 따라서 policy improvement는 original policy가 이미 optimal인 것을 제외하고 엄밀히 말해 더 좋은 policy를 제공해야 한다.
지금까지 이 섹션에서 deterministic policy의 특별한 경우들을 고려했다. 일반적인 경우 stochastic policy \( \pi \)는 각 state s에서 취한 action a인 확률 \( \pi\left( a|s \right) \)를 명시한다. 자세한 내용은 다루지 않겠지만, 사실 이 섹션의 모든 아이디어들은 stochastic policy로 쉽게 확장된다. 특히 policy improvement 정리는 stochastic의 경우에 위에서 언급한대로 진행된다. 뿐만아니라 (4.9)와 같은 policy improvement단계(즉 최대치를 달성하는 action이 여러가지가 있는 경우)에서 stochastic의 경우는 그 중에서 하나의 action을 선택할 필요가 없다. 대신에 각각의 극대화된 action은 새로운 greedy policy에서 선택될 확률의 일부를 가진다. 모든 배분(approtioning) 계획은 모든 하위최대(submaximal) action의 확률이 0인한 허용된다.
그림 4.1의 마지막 행은 stochastic policy에서 policy improvement의 예를 보여준다. 여기서 original policy \( \pi \)는 랜덤 policy이고 새로운 policy \( \pi' \)은 \( v_{\pi} \)에 따른 greedy policy이다. value function \( v_{\pi} \)는 좌측하단에 보이고 가능한 \( \pi' \)의 집합은 우측하단의 표에 보인다. \( \pi' \)의 도표에서 여러개의 화살표가 있는 state들은 여러 action이 (4.9)에서 최대치를 달성하는 state이다. 이러한 action들 사이에서의 확률 배분(apportionment)는 허용된다. 이러한 policy의 경우 state value \( v_{\pi'} \left(s \right) \)는 모든 state \(s \in S \)에 대해 검사를 통해 -1, -2 또는 -3으로 볼 수 있는 반면, \( v_{\pi} \left( s\right) \)는 최대 -14이다. 따라서 \( v_{\pi'} \left( s\right) \geq v_{\pi} \left(s \right) \)는 모든 \( s \in S \)에 대해 policy improvement를 설명한다. 이 경우 새로운 policy \( \pi' \)가 opcimal로 나타나지만, 일반적으로는 improvement만 보장된다.
Reference : Reinforcement Learning : An Introduction
'강화학습 > Reinforcement Learning An Introduction' 카테고리의 다른 글
| Reinforcement Learning 책 읽고 공부하기(4-2) (0) | 2020.12.14 |
|---|---|
| Reinforcement Learning 책 읽고 공부하기(3, Exercise2) (0) | 2020.03.12 |
| Reinforcement Learning 책 읽고 공부하기(3-3) (0) | 2020.03.12 |
| Reinforcement Learning 책 읽고 공부하기(3-2) (0) | 2020.03.09 |
| Reinforcement Learning 책 읽고 공부하기(3, Exercise) (2) | 2020.03.09 |