sutton 교수의 Reinforcement Learning An Introduction을 읽고 공부하기
chapter 2 살펴보기
강화학습 내용 잠깐
강화학습이 기존의 학습방식들과 다른점은 올바른 action을 학습하는 것이 아니라 에이전트가 선택한 action이 얼마나 좋은 action인지 평가한 것을 학습에 사용하는 것이다. 지도학습처럼 어떤 action이 가장 좋은 action인지 알고 시작하는 것이 아니기 때문에 좋은 action을 찾기 위해서는 적극적인 exploration이 필요하다. 여기서 에이전트가 선택한 action에 대해서 피드백을 해주는 두가지 방식이 존재한다.
Evaluative feedback
Evaluative feedback에서는 에이전트가 선택한 action들에 의존적인 피드백 방식이다. 에이전트는 자기가 선택한 action이 best인지 worst인지 모른다. 이번 챕터에서는 이 방식을 사용한다.
Instructive feedback
반면 instructive feedback은 에이전트가 선택한 action과는 독립적인 피드백 방식이다. best or worst action이 무엇인지 알고 있는 방법으로 마치 지도학습처럼 생각할 수가 있다.(이 방식에 대해서는 정확하진 않음.)
K-armed bandit 문제
k개의 슬롯머신들이 있다고 했을 때, 슬롯머신들 중에서 하나의 레버를 당긴다고 해보자. 여기서 하나의 레버를 선택해서 당기는 것을 action으로 한다. 레버를 당긴 후에는 해당슬롯 머신의 stationary probability distribution(정적인 확률분포)에 따라 reward를 받는다. 그러니까 reward의 분포 내에서 랜덤하게 reward를 받는다. 이 문제의 목표는 제한된 횟수 내에서 최적의 레버(action)를 선택해 reward의 기대값을 최대화하는 것이다. 즉 여러 레버를 당겨보면서 가장 reward를 많이 주는 레버를 찾는 것이다.
이제 식을 세워보자, 어떤 시점 t에서 선택한 action을 \( {A}_{t} \)라 하고, 그 때의 reward를 \( {R}_{t} \)라 한다. 이 때 action a의 value는 \( {q}_{*} \left( a \right) \)이고 다음과 같이 표현할 수 있다.

위와 같이 각 action의 value를 안다면 action을 선택할 때 그냥 value가 가장 높은 것을 선택하면 되지만, 이런 action value의 값을 모르고 추정값 \( {Q}_{t} \left(a \right) \)만 안다고 하자. 이 추정값 \( {Q}_{t}\left(a \right) \)를 \( {q}_{*} \left(a \right) \)에 가깝게 만들 수 있다면 가장 좋을 것이다.
우리는 \( {q}_{*}\left(a \right) \)의 값을 알지 못하고 추정값만 알고 있으므로 레버를 선택하는 매 시점 t마다 action value의 추정값이 가장 높은 것들을 선택할 것이다. 이렇게 눈 앞에서 추정값이 가장 높은 action을 선택하는 것이 greedy action이고 exploitation이다. 하지만 exploitation은 단기적인 관점에서 reward를 향상시키는 것이다. 그래서 장기적인 관점에서 추정값을 향상시켜줄 수 있는 exploration이 필요하다. exploration과 exploitation 간의 균형을 맞추는 것은 강화학습에서의 도전 과제이다.
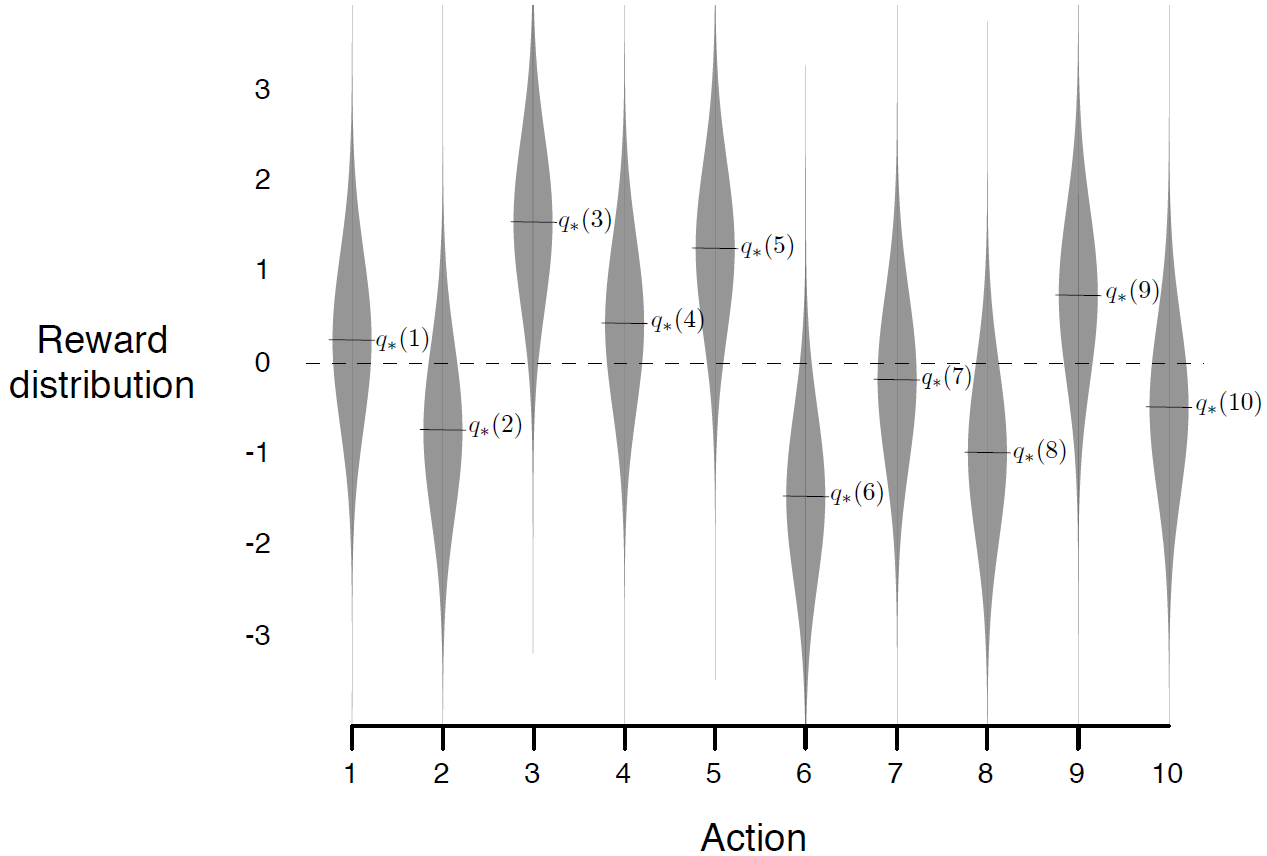
그림은 k-armed bandit 문제의 예제로, 10개 action들의 각각의 rewrad distibution이고 action value의 true value를 나타낸 그래프이다. 10-armed bandit 문제라고 할 수 있을 것이다. 각각의 reward distribution은 mean=\( {q}_{*}\left(a \right) \), var=1인 정규분포다.
\( \epsilon \)-greedy action & greedy action
그렇다면 action value의 추정값은 어떻게 구해야 할까? action의 true value는 그 action을 선택했을 때 받은 reward들의 평균이다. 따라서 에이전트가 실제로 받은 reward들의 평균을 구하는 것이 추정값을 구하는 자연스러운 방법일 것이다.

다음과 같은 식으로 평균을 구할 수가 있다. 만약 분모가 0일경우는 한번도 action을 선택한적이 없다는 뜻이다. 이 때는 기본값(ex. 0)으로 설정한다. 만약 분모가 무한으로 간다면 정말로 많은 action을 해봤다는 뜻이므로 추정값은 true value인 \( {q}_{*} \left(a \right) \)로 수렴할 것이다. 이 방법을 sample-average 방법이라 한다.
어떤 레버를 당길지 고민할 때, 이렇게 구한 추정값들 중 가장 높은 값을 가지는 레버(action)을 선택하는게 greedy action이고 다음과 같이 표현한다.

이 방법은 exploitation 방법이고 우리는 더 나은 추정값을 찾기 위해 exploration을 해야 한다. exploration을 하기 위해서 추정값과 상관없이 \( \epsilon \)의 확률로 랜덤하게 action을 선택하게 한다. 이를 \( \epsilon \)-greedy action방법을 사용한 non-greedy action이라 한다.
위의 10-armed bandit 문제에서 greedy action과 \( \epsilon \)-greedy action을 비교해보자.

총 1000번의 타임스텝을 하는데 \( \epsilon \)-greedy action이 더 나은 성능을 보여줌을 알 수 있다. 그리고 \( \epsilon \)이 작으면 더 시간은 오래 걸리겠지만 더 좋은 action을 찾을 것으로 예상해볼 수 있다.
여기서 만약 reward distribution의 분산이 1이 아니라 10이라면 optimal action을 찾기 위해 더 많은 exploration을 해야할 것이고 만약 분산이 0이면 한번의 greedy action으로 바로 optimal action을 찾을 수 있기 때문에 exploration은 하지 않는게 낫다.
Incremental Implementation
위의 sample-average방법은 계산하기 위해 이전의 모든 reward들을 기억해야한다. 이보다 더 효과적인 방법이 있다. 바로 incremental implemenation을 사용하는 방법이다. 원래는 아래와 같은 식을

Incremental하게 계산하면 다음과 같다.

n=1인 경우 \( {Q}_{2} = {R}_{1} \)이다. 이 계산방법의 일반적인 형태는 아래와 같다.

여기서 Target - OldEstimate 부분을 error라고 한다. 그러니까 업데이트의 목표인 Target과 그전까지의 값인 OldEstimate와의 차이에 Stepsize만큼 곱해서 Target과의 차이를 조금씩 좁혀나가는 것이라고 해석할 수 있다.
이 incremental 계산방법과 sample-average 방법, \( \epsilon \)-greedy를 사용하는 bandit 알고리즘의 수도코드는 다음과 같다.

하지만 이 bandit 문제에도 생각해봐야할 것이 있다. 위의 bandit문제는 reward의 분포가 정적이지만 종종 정적이지 않은(nonstationary) 강화학습 문제가 있다는 점이다.
다음과 같은 예제가 있다. 과거의 reward보다 현재의 reward에 더 많은 가중치를 주는 방법으로 이런 가중치를 주기 위해 stepsize 파라미터에 상수를 사용하는 것이다.

stepsize파라미터는 0~1사이의 값으로, 그 결과 \( {Q}_{n+1} \)은 과거에 받았던 reward들의 가중평균이 된다.

수식2.7을 보면 상수값 \( \alpha \)가 1에 가까워질수록 최근에 받은 reward에 더 많은 가중치를 둔다는 것을 알 수 있다. 각각의 action 마다 stepsize 파라미터를 다양하게 하는 것이 좋을 수 있다. \( {\alpha}_{n}\left(a \right) \), 이렇게 action마다의 stepsize를 함수로 표현할 수 있다. 하지만 이렇게 파라미터가 다양한 경우 true action value에 수렴하지 않을 수도 있다. 확률근사이론에서는 수렴하는데 필요한 조건을 다음과 같이 알려준다.
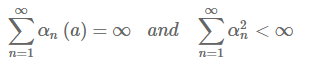
첫번째 조건의 경우 각각의 stepsize 값이 초기값과 임의의 변동성을 극복할 수 있을만큼 충분히 크다는 것을 보여주고 두번째 조건은 결과적으로 stepsize 값이 수렴할 정도로 충분히 작음을 보여준다.
10-armed bandit문제를 풀기 위한 여러가지 방법들을 알아보자
최적의 초기값
앞에서 본 방법은 action value의 초기값 \( {Q}_{1}\left( a \right) \)에 민감하다. sample-average 방법의 경우 모든 action들이 적어도 한번 선택되어 편향은 사라지지만 상수값을 사용한다면 시간이 지남에 따라 편향이 감소하긴 해도 영구적으로 남는다.
Action value의 초기값은 exploration을 시키는데도 사용되는데 앞의 10-armed bandit 문제에서 action value의 초기값이 0이 아니라 +5인 경우를 생각해보자. 그러면 에이전트가 선택한 action이 무엇이든 그 때 받은 reward는 초기값보다 작기 때문에 항상 exploration을 할 것이다.

그림 2.5는 일반적인 greedy action과 초기값을 다르게 준 greedy action을 비교했다. 학습의 초기에는 많은 exploration을 하는 optimistic 방법이 나빠보이지만 결과적으로 더 나은성능을 보여준다. 하지만 이런 초기값은 정적인 문제에는 적용가능하지만 정적이지 않은(nonstationary)문제에는 적합하지 않다. 만약 풀어야하는 문제가 변해 exploration의 필요성이 새로워지면 이 방법은 도움이 되지 않을 것이다.
Upper-Confidence-Bound Action Selection
다음은 UCB action select방법이다. action value의 참값을 구하기 위해서 exploration은 필요하다. \(\epsilon \)-greedy action방법을 소개했는데 실제로 optimal value일 가능성에 따라 non-greedy action을 선택하는것이 좋은 방법일 것이다. action value의 추정값이 그 최대치에 얼마나 가까운지, 그리고 그 추정값이 얼마나 불확실한지(uncertainty)를 고려해 action을 선택한다. 하나의 효과적인 방법은 다음과 같다.
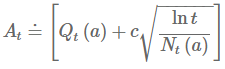
여기서 제곱근은 action value 추정값의 불확실성 또는 분산을 측정한 것이고 c는 exploration의 정도를 나타낸다. 어떤 시점 t에서 action a를 선택하면 N의 값이 증가해 분모가 증가하므로 불확실성은 감소할 것이고, a 이외의 action을 선택하면 분자인 lnt만 증가하고 분모는 증가하지 않아 추정값에 대한 불확실성은 증가할 것이다. 분자에 자연로그를 했으므로 증가폭은 계속해서 작아질 것이다. 결과적으로 모든 action들은 선택이 되겠지만 추정값이 낮거나 자주 선택되지 않은 action들은 선택되는 빈도가 감소한다.

그림은 10-armed bandit에서 두 알고리즘을 비교한 것이다. UCB의 성능이 더 낫지만 UCB는 bandit문제가 아닌 다른 일반적인강화학습 문제에 적용하기 어렵다. 복잡한 nonstationary 문제들이 그 예이고 state가 많을때도 그렇다.
Gradient Bandit Algorithm
여기선는 각 action에 대한 선호도 \( {H}_{t} \)를 본다. 이는 각 action에 대한 선호도(preference)로 선호도가 크면 그 aciton을 더 많이 선택한다. 그렇다고 해서 reward와 관련이 있는 것은 아니고 단지 선호도가 높으면 선택할 확률이 올라간다고 생각하면 된다. 선호도를 고려한 action을 고를 확률은 다음과 같이 \( \pi \)로 나타낼 수 있고 소프트맥스 분포를 따른다.

시점 t에서 action a를 선택할 확률을 위와 같이 파이로 표현한다. soft-max action preference는 확률적 경사 상승법에 기본 아이디어를 두고 있다. 각 시점 t마다 action을 선택하고 reward를 받으면 선호도는 다음과 같이 업데이트한다.

초기에 모든 선호도는 0으로 동일하다. 여기서 \( \alpha \)는 stepsize파라미터이고 \( {\overline{R}}_{t} \)는 시점 t를 제외한 그전까지 reward들의 평균으로 새로 t 시점에서 받은 reward와 비교하는 baseline이다. reward가 baseline보다 높다면 action \( {A}_{t} \)를 선택할 확률은 높아질 것이고 너 낮다면 확률은 낮아질 것이다.

그림 2.7은 10-armed bandit 문제에 적용한 것을 보여준다. basline을 사용하지 않았을 때(상수 0)인경우가 baseline을 적용했을 때보다 상당히 성능이 낮은 것을 볼 수 있다.
Associative Search(Contextual Bandits)
지금까지 본 알고리즘들은 다른 상황들을 고려하지 않는 nonassociative search이다. 하지만 일반적인 강화학습 task는 한개 이상의 상황에서 적절한 policy를 학습하는 것이다. 만약 서로다른 k-armed bandit문제가 여러개가 있다고 했을 때 레버(action)를 선택해야할 때마다 이들 중 하나의 문제를 선택한다고 하면 내가 레버를 선택하려고 할 때마다 true action value는 무작위로 바뀔 것 이다. 이는 마치 nonstationary k-armed bandit 문제처럼 보인다.
Associative search는 k-armed bandit 문제와 full reinforcement learning문제 사이에 있다. full reinforcement learning에서는 policy를 학습하지만 k-armed bandit문제에서는 각 action에 대한 즉각적인 reward만을 고려한다. 만약 action이 즉각적인 reward뿐만 아니라 다음 상황에까지 영향을 미친다면 full reinforcement learning문제라고 할 수 있다.
정리
이번 챕터에서 본 알고리즘들은 exploration과 exploitation간의 균형을 맞추어 k-armed bandit문제를 푸는 방법들이다. \( \epsilon \)-greedy 방법에서는 낮은 확률로 무작위의 action을 선택하고 UCB방법은 deterministic하게 각 시점에서 받은 aciton들 중 하나를 선택하는 것으로 exploration을 한다. Gradient bandit 알고리즘은 action value를 평가하는 것이 아닌 선호도를 이용해 소프트맥스 분포를 사용해서 확률적으로 action을 선택한다.

이런 방법들 중 어떤 방법이 최선인지 고르는 것은 어렵다. 10-armed bandit 문제를 이용해 이 알고리즘들의 성능을 비교한 것은 그림 2.8과 같다. 보면 알겠지만 모든 알고리즘들은 고유의 파라미터 값이 중간 정도에 있을 때 가장 좋은 결과를 보여준다. 이번 챕터에서 살펴 본 단순한 방법들이 현재로써는 최선이지만 exploration과 exploitation 간에 균형을 맞추는 아주 만족스러운 방법은 아니다.
Reference
[1] Reinforcement Learning : An Introduction
'강화학습 > RL Introduction 책 요약' 카테고리의 다른 글
| 유한 state의 Markov Decision Process(Chapter 3) (0) | 2020.05.21 |
|---|---|
| 강화학습이란 무엇인가(Chapter 1) (0) | 2020.05.17 |