sutton 교수의 Reinforcement Learning An Introduction을 읽고 공부하기
Chapter 2
Multi-armed Bandits
강화학습이 다른 타입의 학습방법들과 구분되는 특징은 올바른 action으로 학습하는 것이 아니라 선택한 action을 평가한 것을 훈련 정보로 사용하는 것이다. 이는 좋은 행동을 찾기 위한 적극적인 exploration의 필요성을 말해준다. Evaluative feedback은 에이전트가 선택한 action이 얼마나 좋은지를 말해주지만 이 action이 가능한 best인지 worst인지는 말해주지 않는다. Instructive feedback은 반면에, 실제로 선택한 action과 독립적으로 선택해야 하는 올바른 action을 가리킨다. 이 두 feedback 방식은 꽤 다르다. Evaluative feedback은 내가 선택한 action에 전적으로 의지하는 반면에(내가 선택한 action과 연관이 있음), instructive feedback은 내가 선택한 action과 독립적이다. 이번 챕터에서는 강화학습의 evaluative한 측면에 대해서 배운다.
Evaluative feedback 문제를 k-armed bandit 문제의 단순화 버전으로 풀어본다.
강화학습은 내가 선택한 action을 학습에 대한 정보로 사용, 어떤 action이 가장 좋은 action인지 알고 시작하는 것이 아님
내가 선택한 action에 대해 feedback해주는 방식이 두가지가 있는데 evaluative feedback은 선택한 action이 best인지 worst인지 모름, instructive feedback은 내가 선택한 action과는 별게로 best or worst action이 무엇인지 알고 있음
2.1 A k-armed Bandit Problem
k개의 다른 옵션 또는 action들 중에서 반복적으로 선택하는 문제가 있다. 각각의 선택 후에는 선택한 action의 확률 분포를 참고해 숫자로 된 reward를 받는다. 이 문제의 목표는 reward의 기대값을 최대화하는 것이다.
K-armed bandit 문제의 원래 형태는 k개의 슬롯 머신들의 레버를 당기는 것이다. 각각의 action은 슬롯 머신들의 레버 중 하나를 당기는 것이고, 이 때 reward는 잭팟의 payoff(대가?)다. 반복적인 action 선택을 최고의 레버를 당겨서 잭팟을 많이 터뜨려야 한다.
K-armed bandit 문제에서 각각 k개의 action들은 action을 선택했을 때 reward의 기대값/평균을 준다. 이를 이제부터 action의 value라고 한다. 타임스텝 t에서 선택한 action을 \( {A}_{t} \)라 하고, 그 때의 reward를 \( {R}_{t} \)라 한다. 그러면 어떤 action a의 value를 \( {q}_{*} \left( a \right) \)라 한다. 그러면 action a를 선택했을 때 reward의 기대값은 다음과 같이 표현 가능하다.
$$ {q}_{*} \left(a \right) = E \left[ {R}_{t} | {A}_{t}=a \right] $$
각 action의 value를 안다면 k-armed bandit 문제는 쉽게 풀 수 있다. 각 action을 선택할 때마다 그냥 value가 가장 높은 것을 선택하면 된다. 근데 우리는 action value들의 확실한 값들은 모르고 추정값(estimate)들을 안다고 가정한다. 타임스텝 t에서 action a의 추정(estimated) value는 \( {Q}_{t} \left( a \right) \)이다. 여기서 \( {Q}_{t} \left( a \right) \)를 \( {q}_{*} \left( a \right) \)에 가깝게 하고 싶다.
타임스텝 t에서 action value의 추정값이 가장 높은 것을 선택한다. 이것을 greedy actions라 하고 이러한 action들 중 하나를 선택하는 것을 exploiting이라 한다. nongreedy actions중에서 하나를 선택하는 것은 exploring이라 하는데 exlporing은 nongreedy actoin value들의 추정값들을 향상시킬 수 있다. Exploitation은 한 스텝마다 기대값을 최대화하는 작업이다. 하지만 exploration은 한 스텝이 아닌 장기적인 학습에서 reward의 총합을 더 많이 늘릴 수 있다. 장기적인 학습의 경우 nongreedy action을 explore하는게 greedy action하는 것보다 더 좋다. Reward는 단기학습에서는 exploration을 하는 동안 낮은 값을 갖지만 장기학습에서는 더 높다. 왜냐하면 더 좋은 action을 발견한 후에는 많은 학습을 통해 exploit하기 때문이다. explore와 exploitation은 한번의 action 선택에서 둘 다 할 수 없다. exploration과 expoitation 간의 균형을 맞추는 것은 강화학습에서 도전과제이다. 이 챕터에서는 k-armed bandit 문제를 예제로 사용해 이 문제를 풀어본다.
이 단원에서는 k-armeed Bandit 문제를 예제로 사용해 공부함. k개의 슬롯 머신에서 하나의 레버를 당기는 것을 action이라고 하면 action을 선택한 후에는 그에 맞는 reward를 받음. 이 문제의 목표는 k개의 슬롯머신에서 레버를 여러번 당겨 reward의 기대값을 최대화 하는 것
action을 선택하면 reward를 받고 이 기대값/평균을 action의 value라 함, \( {q}_{*} \left(a \right) = E \left[ {R}_{t} | {A}_{t}=a \right] \)
그리고 타임스템 t에서 action a의 추정값은 \( {Q}_{t} \left( a \right) \)임, \( {Q}_{t} \left( a \right) \)를 \( {q}_{*} \left( a \right) \)에 가깝게 만들자!
greedy action : action value의 추정값이 가장 높은 것이 greedy action이고 이 것을 선택하는게 exploiting
nongreedy action : nongreedy action 중에서 action을 선택하는 것이 exploring, 장기적인 학습에서는 exploring을 하는 것이 좋음
2.2 Action-value Methods
action의 value를 추정하고 action을 선택하기 위해 추정값을 이용한다. 이를 action-value 방법이라 부른다. action의 true value는 그 action을 선택했을 때 받을 reward의 평균이라는 것을 기억하자. 이를 추정하는 자연스러운 방법은 실제로 받은 reward들의 평균으로 계산하는 것이다.
$$ {Q}_{t}\left( a \right) \doteq \frac{ \textrm{sum of rewards when a taken prior to t} }{ \textrm{ number of times a taken prior to t }} = \frac{ \sum_{t-1}^{i=1} {R}_{i} \cdot {1}_{ {A}_{i}=a } }{ \sum_{t-1}^{i=1} {1}_{ {A}_{i}=a } } $$
분모가 0이라면 \( {Q}_{t} \left( a \right) \)를 0 같은 기본 value로 설정한다. 분모가 무한이라면 \( {Q}_{t} \left( a \right) \)는 \( {q}_{*}\left( a \right) \)로 수렴한다. 이를 action value를 추정하기 위한 sample-average 방법이라 부른다. 이 추정값이 어떻게 action을 선택하는데 사용될까?
가장 단순한 action 선택 방법은 가장 높은 추정값을 가진 action을 선택하는 것, 그게 바로 greedy action이다. greedy action 선택방법은 다음과 같이 표현한다.
$$ {A}_{t} \doteq \underset{a}{argmax} {Q}_{t}\left( a \right) $$
greedy action 선택은 항상 즉각적인 reward를 exploit한다. 더 나은 action을 찾기 위해 더 낮은 값을 주는 action을 explore하지는 않는다. greedy action에서 explore를 할 수 있는 간단한 방법은 작은 확률 \( \epsilon \)을 이용해 랜덤하게 action value의 추정값과 관계없이 모든 action을 동일한 확률 \( \epsilon \)으로 선택하는 것이다. 이 방법을 \( \epsilon \)-greedy방법을 사용한 non-greedy action 선택이라 한다. 이 방법의 장점은 모든 action들을 시간이 흐름에 따라 \( {Q}_{t}\left( a \right) \)가 \( {q}_{*}\left( a \right) \)로 수렴할 수 있게 해준다. 이는 optimal action을 선택할 확률이 1-\( \epsilon \)보다 더 큰값으로 거의 확실하게 수렴함을 의미한다.
action value를 실제로 받은 reward들의 평균으로 추정.이 평균으로 추정하는 방법을 sample-average방법이라 하고 식은 위와 같음.
여기서 분모가 0이면 reward를 받은적이 없는 것이고 0을 기본 value로 설정. 분모가 무한대로 간다면 \( {Q}_{t} \left( a \right) \)는 \( {q}_{*}\left( a \right) \)로 수렴, action의 reward를 sample-average방식으로 추정한 것은 aciton의 기대값으로 수렴한다는 말(?)
greedy actoin : 가장 높은 추정값 가진 action을 선택 explore하지 않음
\( \epsilon \)-greedy action : greedy action에서 explore를 할 수 있게 만든 방법. 확률 \( \epsilon \)을 이용해 모든 action을 동일한 확률로 선택. non-greedy action방법임
2.3 The 10-armed Testbed
greedy와 \( \epsilon \)-greedy action-value방법의 상대적인 효과를 간략하게 평가하기 위해 테스트 문제를 이용해 숫자로 이 둘을 비교한다. k=10일때 2000번의 반복을 통해 얻은 reward의 분포. action value \( {q}_{*}\left( a \right) \)는 정규분포(mean=0, var=1)에 따라서 선택되었다. 타임스텝 t에서 선택한 action \( {A}_{t} \)이면 mean이 \( {q}_{*} \left( {A}_{t} \right) \), var이 1인 정규분포라고 할 수 있다.
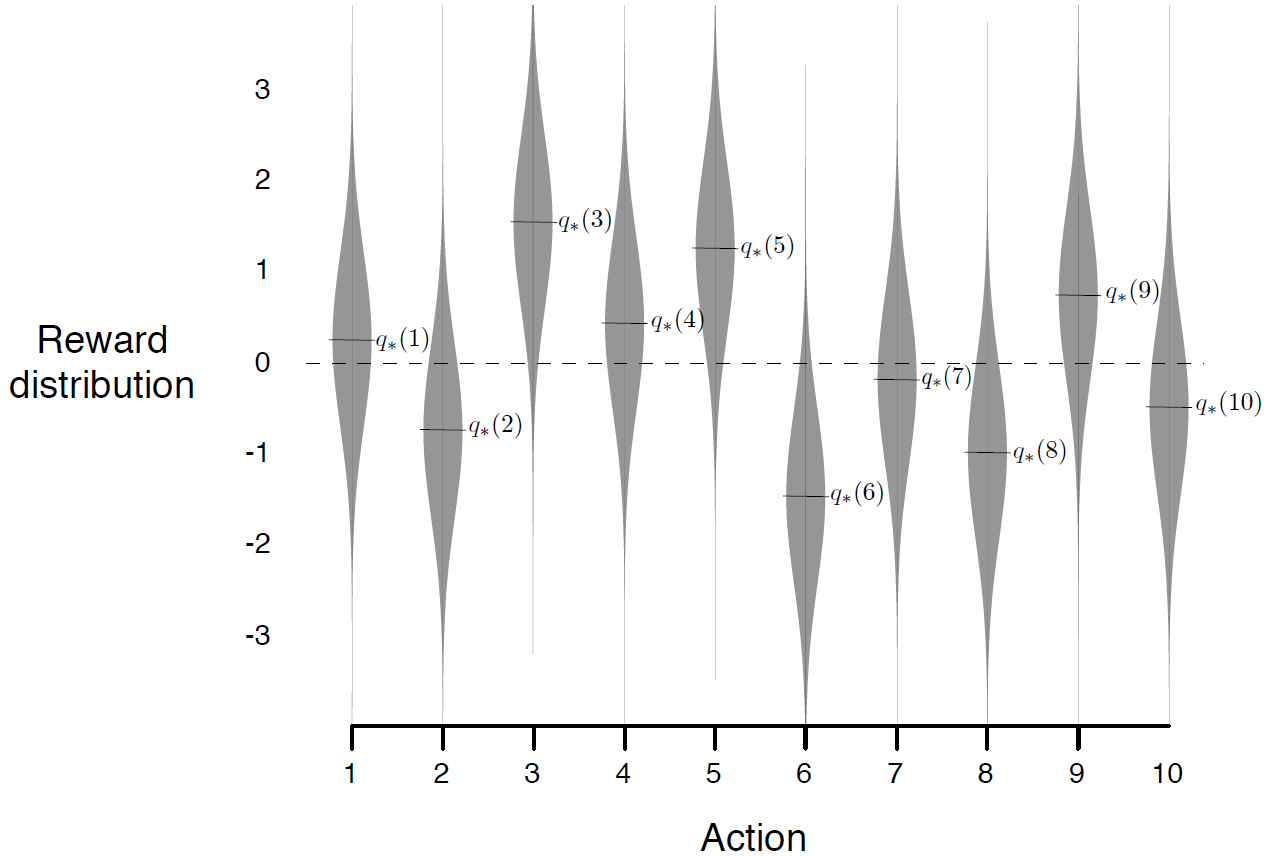
이 예제를 10-armed testbed라 부른다. 1000 타임스텝의 경험으로 개선
그림 2.2는 10-armed testbed 예제에서 greedy 방법과 \( \epsilon \)-greedy 방법(\( \epsilon \)=0.01, \( \epsilon \)=0.1)이다. 위쪽의 그래프가 경험(타임스텝)에 따른 reward의 기대값이 증가하는 것을 보여준다. greedy 방법은 학습의 아주 초기에는 다른 방법들보다 약간 더 빠르게 개선된다. 하지만 이 방법은 testbed에서 average reward의 최대값이 1.55정도 이지만 1에 수렴된다. greedy 방법은 긴 학습에서는 상당히 나쁘다.
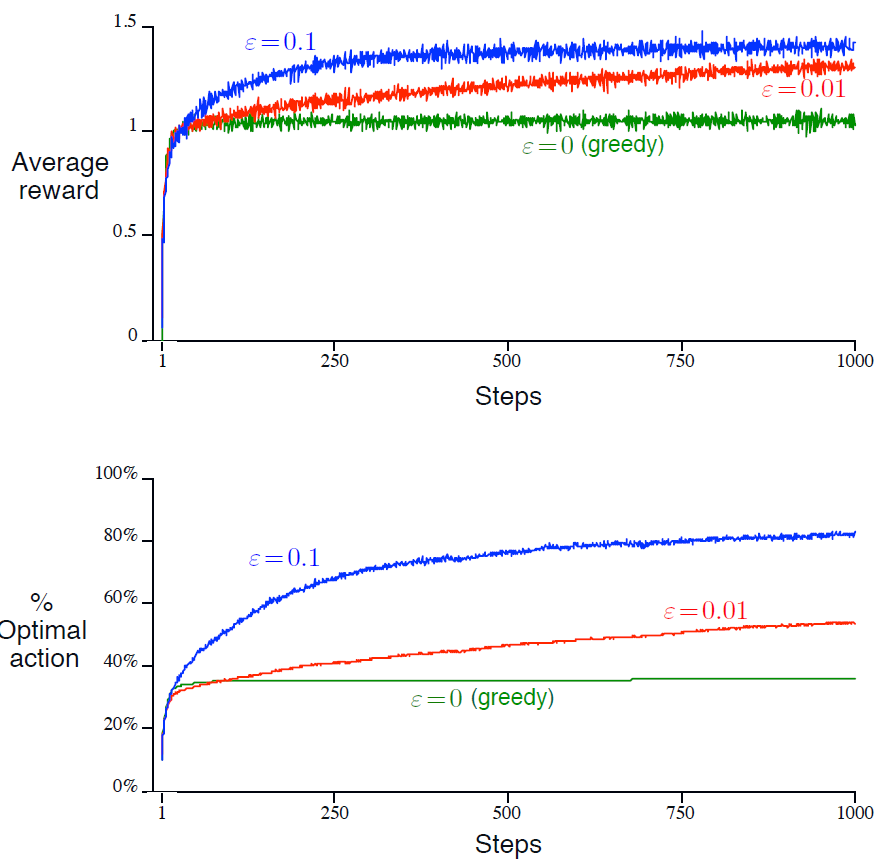
아래의 그래프에서 greedy 방법은 작업의 대략 1/3정도에서 optimal action을 찾았다. 결과적으로 보자면 \( \epsilon \)-greedy 방법은 explore를 계속하고 개선시켜 optimal action을 찾을 기회가 더 많아져 성능이 더 좋다. \( \epsilon \)=0.1일때 explore를 많이하고 보통 초기에 optimal action을 찾는다. 하지만 그 action을 시간의 91% 이상 선택하지는 않았다.(but it never selected that action more than 91% of the time, 이게 뭔소리인가 싶음). \( \epsilon \)=0.01일때는 더 느리게 향상시키지만 결과적으로 \( \epsilon \)=0.1일 때보다는 더 낫다.
이 \( \epsilon \)-greedy 방법의 장점은 문제가 무엇이냐에 따라 다르다. reward의 분산이 1이 아니라 10으로 더 크다면 노이즈가 낀 reward이므로 optimal action을 찾기 위해 더 많이 exploration을 해야한다. 반면에 reward의 분산이 0일경우 greedy 방법은 각 action을 한번만 하더라도 true value를 알 수 있다. 이러면 greedy 방법이 explore를 하지 않으므로 optimal value를 찾는데 더 낫다.
greedy와 \( \epsilon \)-greedy를 비교하는 그래프
그림 2.1은 각 action마다 받을 reward들의 분포가 정규분포임을 나타냄.
그림 2.2를 보면 \( \epsilon \)-greedy 방법이 greedy방법보다 평균 reward가 더 높음을 알 수 있음. optimal action을 보면 \( \epsilon \)=0.1일 때보다 \( \epsilon \)=0.01일 때 optimal action을 더 많이 선택한다고 함.
근데 만약 reward의 분산이 0이라면 explore를 하지 않는 greedy 방법이 나을 것임
Reference : Reinforcement Learning : An Introduction
'강화학습 > Reinforcement Learning An Introduction' 카테고리의 다른 글
| Reinforcement Learning 책 읽고 공부하기(2-4, Exercise) (0) | 2020.02.21 |
|---|---|
| Reinforcement Learning 책 읽고 공부하기(2-3) (0) | 2020.02.21 |
| Reinforcement Learning 책 읽고 공부하기(2-2) (0) | 2020.02.17 |
| Reinforcement Learning 책 읽고 공부하기(1-2, Exercise) (0) | 2020.02.11 |
| Reinforcement Learning 책 읽고 공부하기(1) (0) | 2020.02.09 |