sutton 교수의 Reinforcement Learning An Introduction을 읽고 공부하기
2.7 Upper-Confidence-Bound Action Selection
action-value 추정치의 정확도가 항상 불확실하기 때문에 exlporation은 필요하다. \( \epsilon \)-greedy action 선택은 non-greedy action을 선택할 수 있게 한다. 실제로 optimal일 가능성에 따라 non-greedy action을 선택하는 것이 좋다. 여기서 추정치가 최대치에 얼마나 근접한지, 그리고 그 추정치의 부확실성을 고려해 action을 선택한다. 이렇게 action을 선택하는 하나의 효과적인 방법은 아래와 같다.
$$ {A}_{t} \doteq \left[ {Q}_{t}\left( a \right) + c\sqrt{ \frac{\ln t}{{N}_{t}\left( a \right)} } \right] $$
\(\ln t \)는 자연로그를, \( {N}_{t}\left(a \right) \)는 시각 t까지 선택된 action의 개수이다. c는 exploration의 정도를 나타낸다. N이 0일 경우 action a는 최대화된 action으로 간주한다.
이 upper confidence bound(UCB) action 선택의 아이디어에서 루트는 action a value 추정치의 불확실성 또는 분산을 측정한 것이다. 각 시각마다 a를 선택하면 분모인 \( {N}_{t} \left( a \right) \)는 증가해 불확실성(uncertainty)은 감소할 것이다. 한편 a 이외의 다른 action이 선택되면 분자의 t만 증가하고 분모는 증가하지 않아 추정치 불확실성(uncertainty estimate)은 증가한다. 자연로그를 사용했으므로 증가폭은 계속 작아지지만 bound가 제한되지는 않는다. 즉 결과적으로 모든 action들은 선택이 되지만 예상(estimate) value가 낮거나 자주 선택되는 action은 시간이 지남에 따라 빈도가 감소하면서 선택된다.
10-armed testbed에서 UCB를 사용한 결과는 그림 2.4와 같다. UCB의 성능이 더 낫지만, UCB는 \( \epsilon \)-greedy보다 bnadit 문제가 아닌 다른 일반적인 강화학습에 적용하기 더 어렵다. Section 2.5보다 더 복잡한 nonstationary 문제들이 그렇다. 또 다른 어려움은 state가 많은 경우이다.
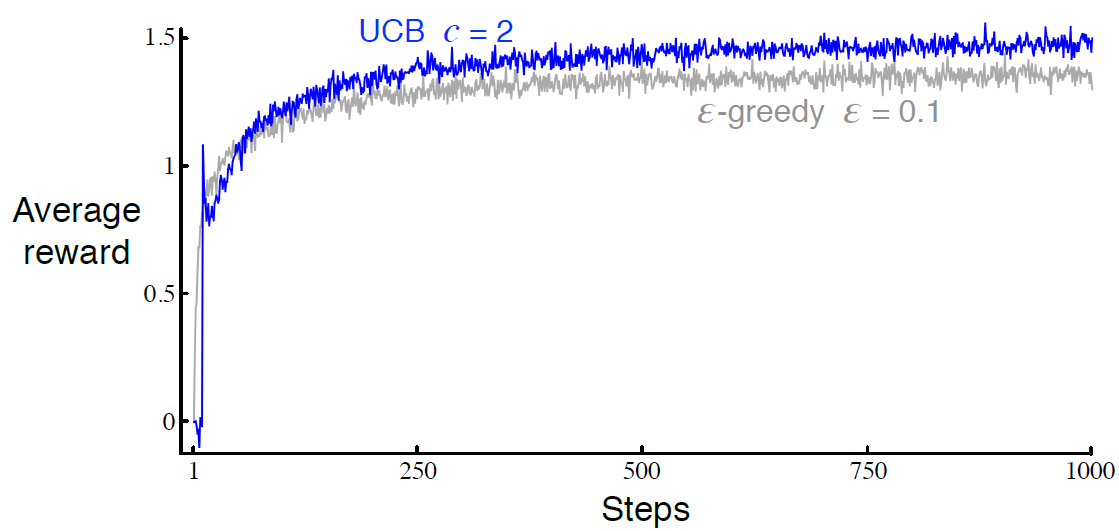
현재 action value estimate값이 참값인지 모르기 때문에 exploration은 필요함. \( \epsilon \)-greedy action의 경우 non-greedy action을 강제함. exploration을 위해 non-greedy action에서 선택하는게 좋은데 왜냐하면 이 action들이 실제 optimal일 수도 있고 estimate값들을 최대화시킬 수도 있기 때문임. 그리고 이렇게 action을 선택하는 방법이 위의 식임.
식에서 루트부분이 action a value estimate의 불확실성(uncertainty) 또는 분산(variance)임.
그리고 자연 로그를 쓰는 이유: 모든 action들은 결국 선택됨 즉, 낮은 value estimate를 주는 action 또는 이미 자주 선택된 action들은 시간이 지날수록 덜 선택함.
UCB 알고리즘 또한 탐험을 수행하게 해주는 알고리즘이라 할 수 있음.
2.8 Gradient Bandit Algorithms
이 챕터에서는 action value를 estimate하고 그 값을 action을 선택하는데 이용하는 방법을 본다. 각 action에 대한 수치적 선호도(preference)를 \( {H}_{t}\left( a \right) \)로 표시한다. preferece가 더 크면 그 action을 더 많이 선택한다. 하지만 preference가 reward로 해석되진 않는다. 오직 하나의 action이 다른 action보다 상대적으로 더 선호된다는 것이다. 만약 모든 action의 선호도에 1000을 더한다면 action의 선택 확률에 영향을 미치지 않을 것이다. 아래의 soft-max distribution 참고.
$$ Pr \left\{ {A}_{t}=a \right\} \doteq \frac{e^{{H}_{t} \left( a \right)} }{ \sum_{b=1}^{k} e^{ {H}_{t} \left( b \right) } } \doteq {\pi}_{t} \left( a \right) $$
여기서 \( {\pi}_{t} \left( a \right) \)는 시각 t에서 action a를 선택할 확률이다. 처음에는 모든 action의 preference는 모두 같다. 그러니까 모든 action들의 선택될 확률은 같다.
soft-max action preference는 확률적 경사 상승법에 기본 아이디어를 두고 있다. 각 스텝마다 action \( {A}_{t} \)를 선택하고 reward \( {R}_{t} \)를 받으면 action preference는 다음과 같은 식으로 업데이트된다.
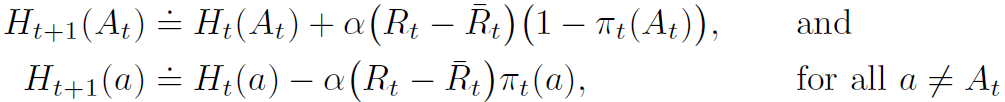
\( \alpha \) > 0인 스텝사이즈 파라미터, \( {\overline{R}}_{t} \in \mathbb{R} \)는 모든 시각 t를 제외한 reward들의 평균. section 2.4처럼 incremental하게 계산 가능하다. \( {\overline{R}}_{t} \)는 reward와 비교하는 baseline이다. reward가 baseline보다 높다면 \( {A}_{t} \)를 선택할 확률은 더 높아진다. reward가 baseline보다 작다면 확률은 작아진다.
그림 2.5는 10-armed testbed에 gradient bandit 알고리즘의 결과를 보여준다. 평균이 0이 아닌 +4인 정규분포에서 선택된 참 기대 보상(true expected reward)이다. 이 모든 reward들의 shifting up(상향이동)은 reward baseline 때문에 gradient bandit 알고리즘에 전혀 영향을 미치지 않는다. 하지만 baseline이 생략된 경우( 상수 0인 경우), 성능이 상당히 낮아졌음을 볼 수 있다.
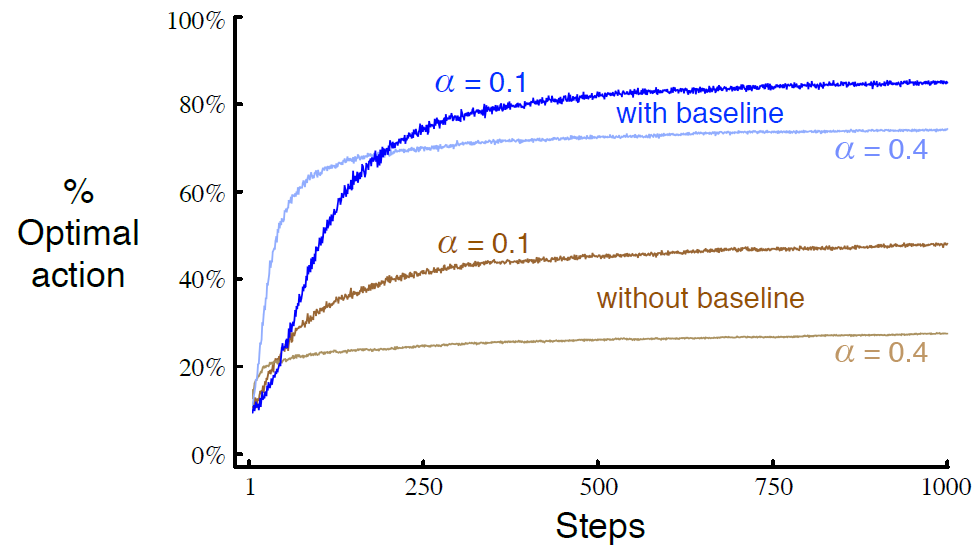
action value를 평가하는 여러가지 방법을 봤는데 여기서는 preference를 고려하는 법을 배움. 각 action마다의 prefenrece를 \( {H}_{t} \left( a \right) \)로 표시. preference는 단순히 action에 대한 선호도임.
그리고 이 preference를 고려해 소프트맥스 분포를 사용해서 각 action을 선택할 확률인 \( \pi \)로 표현함. 각 스텝마다 action과 reward를 이용해 action의 preference를 확률적 경사하강법(stochastic gradient ascent)로 업데이트할 수 있음.
여기서 \( {\overline{R}}_{t} \)는 시각 t를 제외한 이전에 받은 모든 reward들의 평균으로 baseline이라고 부름. 새롭게 받은 reward가 baseline보다 크면 action의 확률은 증가할 거시고 낮으면 확률은 내려갈 것임.
2.9 Associative Search (Contextual Bandits)
지금까지는 nonassociative 작업이였다. 이 작업들에서 learner들은 작업이 stationary일 때는 최선의 single action을 찾으려고 하고 작업이 nonstationary일 때는 최선의 action을 추적하려고 한다. 일반적인 강화학습 작업은 한 개 이상의 상황(situation)이 있고 목표는 policy를 배우는 것이다. 여기서 policy는 action을 각 상황에 맞는 최선의 action으로 상황에 매핑시키는 것을 말한다. 전체 문제의 단계를 설정하기 위해 nonassociative 작업이 associative 설정으로 확장되는 간단한 방법을 설명한다.
하나의 예제로 서로다른 k-armed bandit 문제가 있다고 했을 때 각 스텝마다 이들 중 하나를 선택한다. 따라서 bandit 문제는 한스텝에서 다른 스텝으로 갈때마다 무작위로 바뀐다. 이는 한스텝에서 다른 스텝으로 갈 때마다 참 action value가 랜덤하게 바뀌는 single nonstationary k-armed bandit문제처럼 보인다.
Associative search 작업은 최선의 action을 찾기 위해 시행착오를 거치며 학습한다. 그리고 이 action들을 최선의 상황과 association 시킨다. Associative search 작업은 k-armed bandit 문제와 완전한 강화학습 문제 사이에 있다. 완전한 강화학습 문제는 policy를 학습하지만 k-armed bandit 문제에서 각 action은 오직 즉각적인 reward에만 영향을 미친다. 만약 action이 reward뿐만 아니라 다음 상황에 까지 영향을 미친다면 완전한 강화학습 문제라고 할 수 있다.
associative search는 잘 이해가 안되는 부분이긴 한데 간단하게 nonassociative문제를 associative하게 푸는 법?
policy를 학습하지만 action이 즉각적인 reward에만 영향을 미치는게 associative search인듯?
2.10 Summary
이번 챕터에서 본 것들은 exploration과 exploitation 사이의 균형을 맞추는 간단한 방법들이다. \( \epsilon \)-greedy 방법은 시간의 작은 부분을 무작위로 선택한다...?(choose randomly a small fraction of the time, 이건 뭔소리인지 모르겠는데 action을 무작위로 선택하는 거였음), 반면에 UCB 방법은 deterministically지만 각 단계에서 적은 수의 샘플들을 받은 action들을 미묘하게 선호해 exploration을 한다. Gradiendt bandit 알고리즘은 action value를 평가하는 것이 아닌 action preference를 평가해 더 preferred 된 action을 soft-max 분포를 사용해 확률적으로 선택한다.
이런 방법들 중 어떤게 가장 최선인지는 어려운 질문이다. 우리는 10-armed testbed를 이용해 이것들의 성능을 비교해봤다. 아래의 그래프를 통해 알고리즘과 파라미터 세팅에 따른 성능을 보여준다. 그림 2.6은 이번 챕터에서 배운 다양한 bandit 알고리즘들과 각 함수의 고유한 파라미터가 x축에 나와있다. 이런 그래프를 parameter study라 부른다. 모든 알고리즘들은 고유의 파라미터 값들의 중간정도에서 가장 좋은 결과를 보여준다.
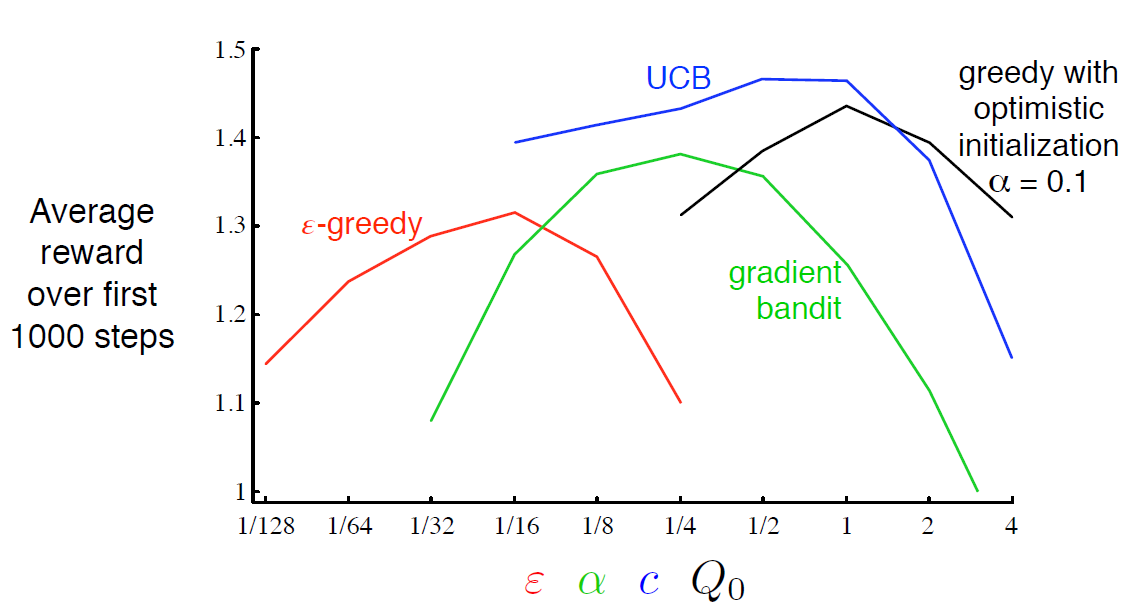
이 챕터에서 살펴본 단순한 방법들이 현재로서는 최선이지만 exploration과 exploitation간에 균형을 맞추는 아주 만족스러운 방법은 아니다.
K-armed bandit 문제에서 exploration과 exploitation 간의 균형을 맞추는 잘 알려진 방법은 Gittins index라 불리는 action value를 계산하는 것이다. 이 방법은 가능한 문제들에 대해서 이전의 분포를 정확히 알고 있어야 하지만 직접적으로 최적의 해결방법을 준다. 또한 이 방법은 이 책의 나머지 부분에서 배울 완전한 강화학습을 일반화하는 것처럼 보이진 않는다.
Gittins-index는 베이지안 방법의 예이다. action value에 대한 처음 분포를 알고 있다고 가정하고 각 스텝 후에 정확하게 분포를 업데이트한다. 보통 업데이트 계산식은 복잡하지만 특별한 분포(conjugate priors라 부르는)에서는 쉽다.
여기까지만 정리
Reference : Reinforcement Learning : An Introduction
'강화학습 > Reinforcement Learning An Introduction' 카테고리의 다른 글
| Reinforcement Learning 책 읽고 공부하기(2-5, Exercise) (1) | 2020.02.24 |
|---|---|
| Reinforcement Learning 책 읽고 공부하기(2-4, Exercise) (0) | 2020.02.21 |
| Reinforcement Learning 책 읽고 공부하기(2-2) (0) | 2020.02.17 |
| Reinforcement Learning 책 읽고 공부하기(2) (0) | 2020.02.15 |
| Reinforcement Learning 책 읽고 공부하기(1-2, Exercise) (0) | 2020.02.11 |