sutton 교수의 Reinforcement Learning An Introduction을 읽고 공부하기
2.4 Incremental Implementation
모든 action-value의 추정값은 관찰한 reward들의 sample average값이다. 이러한 평균을 효과적으로 계산할 수 있는 방법을 알아본다. 단일 action에만 집중하기 위해 표기를 단순화한다. \( {R}_{i} \)는 i번째 action을 선택한 후 받는 reward다. \( {Q}_{n} \)은 n-1번째까지 action을 선택한 후의 action value의 추정값이다. 아래와 같이 쓸 수 있다.
$$ {Q}_{n} \doteq \frac{ {R}_{1}+{R}_{2}+ \cdot\cdot\cdot + {R}_{n-1} }{ n-1 } $$
모든 reward들을 저장해 계산하는 방법대신 incremental 공식을 사용해 average들을 업데이트한다. 주어진 \( {Q}_{n} \), n번째 reward \( {R}_{n} \), 모든 n reward들의 새로운 평균은 다음과 같이 계산한다.
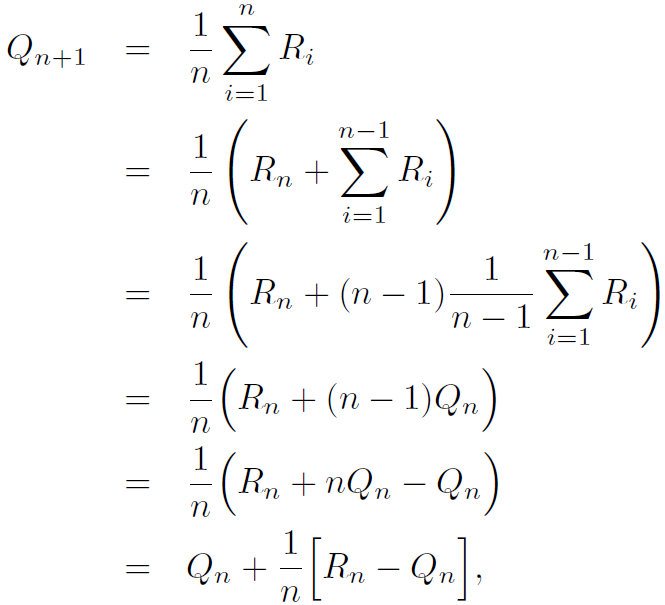
n=1인 경우에는 임의의 \( {Q}_{1} \)에 대해 \( {Q}_{2}={R}_{1} \)이다. 위의 구현 방법은 오직 \( {Q}_{n}\)과 n에 대해서만 계산하면 되므로 새롭게 얻는 reward들에 대해서 작은 계산만 하면 된다.
위의 계산방법의 일반적인 형태가 아래와 같다.
$$ NewEstimate \leftarrow OldEstimate + StepSize \left[ Target - OldEstimate \right] $$
\( \left[ Target - OldEstimate \right] \), 이 식은 추정값에서 error를 나타낸다. error는 "Target"을 향해 한 스텝씩 진행할 때마다 감소한다. Target은 움직여야 하는 바람직한 방향을 가리킨다고 가정한다. 예를 들어 위의 케이스에서는 target은 n번째 reward다.
Incremental 방법에 사용되는 StepSize 파라미터는 타임스텝마다 변한다. aciton a에서 n번째 reward는 step-size 파라미터로 \( \frac{1}{n} \)을 사용한다. 이 책에서는 step-size 파라미터를 \( \alpha \)로 하고 좀 더 일반적으로 \( {\alpha}_{t} \left( a \right) \)로 표시한다.
incremental 계산과 sample average, \( \epsilon \)-greedy action을 사용하는 bandit 알고리즘의 수도코드는 아래와 같다.

sample-average 방식으로 reward의 평균을 구하는 것을 incremental하게 구현한 것으로 계산 및 메모리의 효율성에 도움이 된다고 함.
이걸 일반화시킨게 \( NewEstimate \leftarrow OldEstimate + StepSize \left[ Target - OldEstimate \right]
\) 이거인데 여기서 target-oldestimate가 error임.
그리고 스텝사이즈 파라미터 역시 1/n이 아니라 \( \alpha \)로 고정.
해석해보자면 여태까지 계산한 평균(OldEstimate)과 새로 받은 reward(Target)의 차가 error고 이 error를 얼마만큼 반영할 것인가가 스텝사이즈 파라미터 \( \alpha \)라고 할 수 있음.
2.5 Tracking a Nonstationary Problem
위의 bandit 문제에서는 reward의 확률이 시간이 지나도 변하지 않는다. 하지만 종종 정적이지 않은(nonstationary) 강화학습 문제를 만난다. 과거(long-past)의 reward보다 현재의 reward에 더 많은 가중치를 주는 예제가 있다. 이를 수행하는 잘 알려진 방법은 step-size 파라미터에 상수값을 사용하는 것이다. 위의 incremental 업데이트 방법은 다음과 같이 수정될 수 있다.
$$ {Q}_{n+1} \doteq {Q}_{n} + \alpha \left[ {R}_{n} - {Q}_{n} \right] $$
step-size 파라미터 \( \alpha \)는 0~1사이 상수이다. 그 결과 \( {Q}_{n+1} \)은 과거 reward들의 가중 평균이 되고 초기 추정치는 \( {Q}_{1} \)으로 다음과 같이 쓸 수 있다.
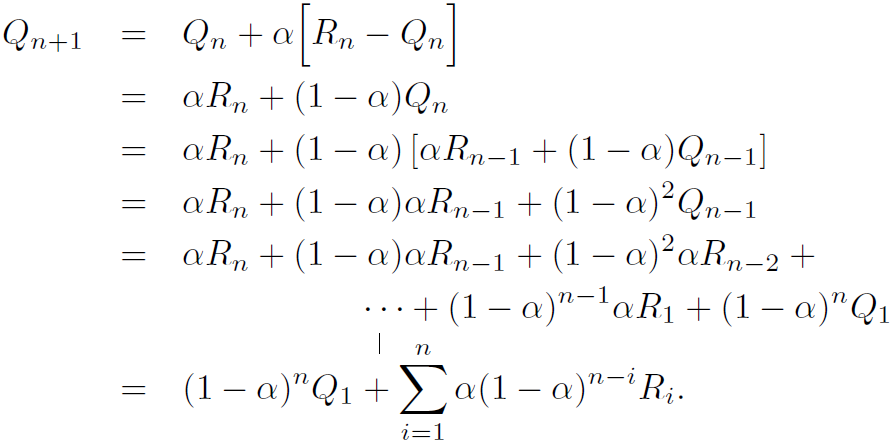
이 것을 가중 평균(weighted average)라 부른다. 1-\( \alpha \)가 1 보다 작은경우 \( {R}_{i} \)의 가중치값은 reward가 증가할 수록 감소한다. 만약 1-\( \alpha \)=0일 경우, 마지막 reward인 \( {R}_{n} \)만 남게된다 왜냐하면 \( 0^{0} \)=1이기 때문이다. 따라서 때때로 exponential recency-weighted average라고 부른다.
때때로 각각의 스텝마다 step-size 파라미터를 다양하게 하는 것이 편하다. step-size 파라미터를 다음과 같이 n번째 action마다 다르게 선택할 수 있다, \( {\alpha}_{n} \left( a \right) \). sample-average 방법에서 \( {\alpha}_{n} \left( a \right) = \frac{1}{n} \)이고 이는 true action value에 수렴할 수 있게 해준다. 당연하게도 파라미터가 다양한 경우, \( \left\{ {\alpha}_{n} \left( a \right) \right\} \) 반드시 수렴하지는 않는다. 확률 근사 이론에서는 확률 1로 수렴하는데 필요한 조건을 알려준다.
$$ \sum_{n=1 }^{\infty} {\alpha}_{n} \left( a \right) = \infty \: \: \: \: and \: \: \: \: \sum_{n=1}^{\infty} \alpha_{n}^{2} < \infty $$
첫번째 조건의 경우 하나의 step이 초기 조건과 임의의 변동서을 극복할만큼 충분히 큼을 보여준다. 두번째 조건은 결과적으로 step이 수렴할 정도로 충분히 작음을 보여준다.
Sample-average의 \( {\alpha}_{n} \left( a \right) = \frac{1}{n} \)일 때는 위의 두가지 조건을 만족해 수렴하지만 \( {\alpha}_{n} \left( a \right) = \alpha \)와 같은 상수일 때는 두번째 조건을 만족하지 못해 수렴하지 못하고 최근에 받은 reward에 따라 변동한다.(?)
위의 sample-average 방식에서 스텝사이즈 파라미터를 상수로 고정시킨게 nonstationary한 강화학습 문제에 더 어울린다고 말하는 듯 함. 이렇게 상수 \( \alpha \)로 바꾸고 식을 정리한 것이 weighted average(가중 평균)으로 reward마다 가중치를 곱함.
각각의 스텝사이즈 마라미터를 다양하게 하는 법이 존재. 스텝사이즈를 1/n으로 했을 때는 참 action value로 수렴하는데 다양하게 했으면 수렴하지 않을 수도 있음. 위의 시그마 수식 두개가 참 action value로 수렴하는 조건인듯.
2.6 Optimistic Initial Values
앞에서 본 방법들은 action-value의 초기(추정)값, \( {Q}_{1} \left( a \right) \)에 민감하다. 통계학적인 용어로 초기(추정)값에 의해 편향(biased)되어 있다고 할 수 있다. 앞의 sample-average 방법에서는 모든 action들이 적어도 한 번 선택되어 편향이 사라졌다. 하지만 상수 \( \alpha \)를 사용한다면 시간이 지남에 따라 감소하긴 하지만 편향은 영구적이다.
Action-value의 초기값은 exploration을 하는데도 사용된다. 앞의 10-armed testbed에서 action-value의 초기값을 0이 아닌 모두 +5했다고 가정해보자. 이 문제에서 \( {q}_{*} \left( a \right) \)는 정규분포(mean=0, var=1)에서 선택됐다. 이 경우 처음으로 선택한 action의 reward는 처음의 추정값보다 작기 때문에 학습을 하는 에이전트는 다른 action을 선택한다.
그림 2.3은 10-armed testbed에서 \( {Q}_{1} \left( a \right) = +5 \)을 사용한 greedy 방법의 성능을 보여준다. 비교를 위해 \( {Q}_{1} \left( a \right) = 0 \)인 \( \epsilon \)-greedy 방법도 같이 그렸다. 학습의 초기에는 optistic 방법이 더 나빠보이지만 이는 explore를 많이 해서 그런 것이다. 하지만 결과적으로 exploration 때문에 더 나은 성능을 보여준다. 이는 stationary 문제에서는 적용 가능하지만 nonstationary 문제에는 적합하지 않다. 왜냐하면 exploration을 위한 추진력은 본질적으로 일시적이기 때문이다. 만약 풀어야하는 문제가 변해 exploration의 필요성이 새로워지면(renewed) 이 방법은 도움이 되지 않는다. 실제로 특별한 방법으로 초기 조건에 초점을 둔 방법은 일반적인 nonstationary 경우에 도움이 되지 않을 것이다.
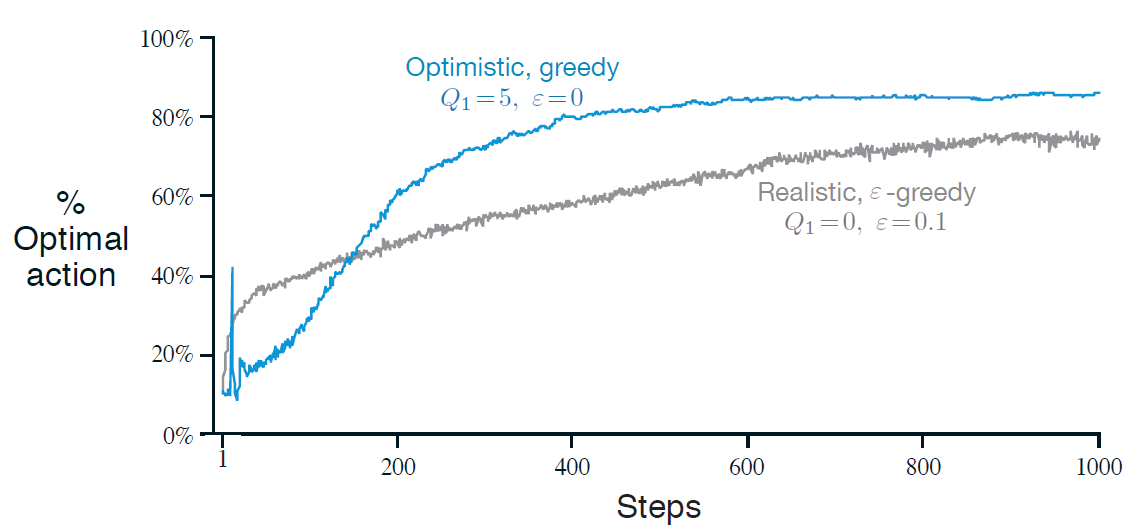
앞에서 본 방식(sample-average 방식과 weighted average 방식 두개를 말하는 건가(?))들은 action-value의 초기값에 민감함. 앞의 예제에서 초기값을 0이 아닌 +5라고 했다고 가정하면 그림처럼 optimal action을 찾을 확률이 증가할 수 있음.
Reference : Reinforcement Learning : An Introduction
'강화학습 > Reinforcement Learning An Introduction' 카테고리의 다른 글
| Reinforcement Learning 책 읽고 공부하기(2-4, Exercise) (0) | 2020.02.21 |
|---|---|
| Reinforcement Learning 책 읽고 공부하기(2-3) (0) | 2020.02.21 |
| Reinforcement Learning 책 읽고 공부하기(2) (0) | 2020.02.15 |
| Reinforcement Learning 책 읽고 공부하기(1-2, Exercise) (0) | 2020.02.11 |
| Reinforcement Learning 책 읽고 공부하기(1) (0) | 2020.02.09 |